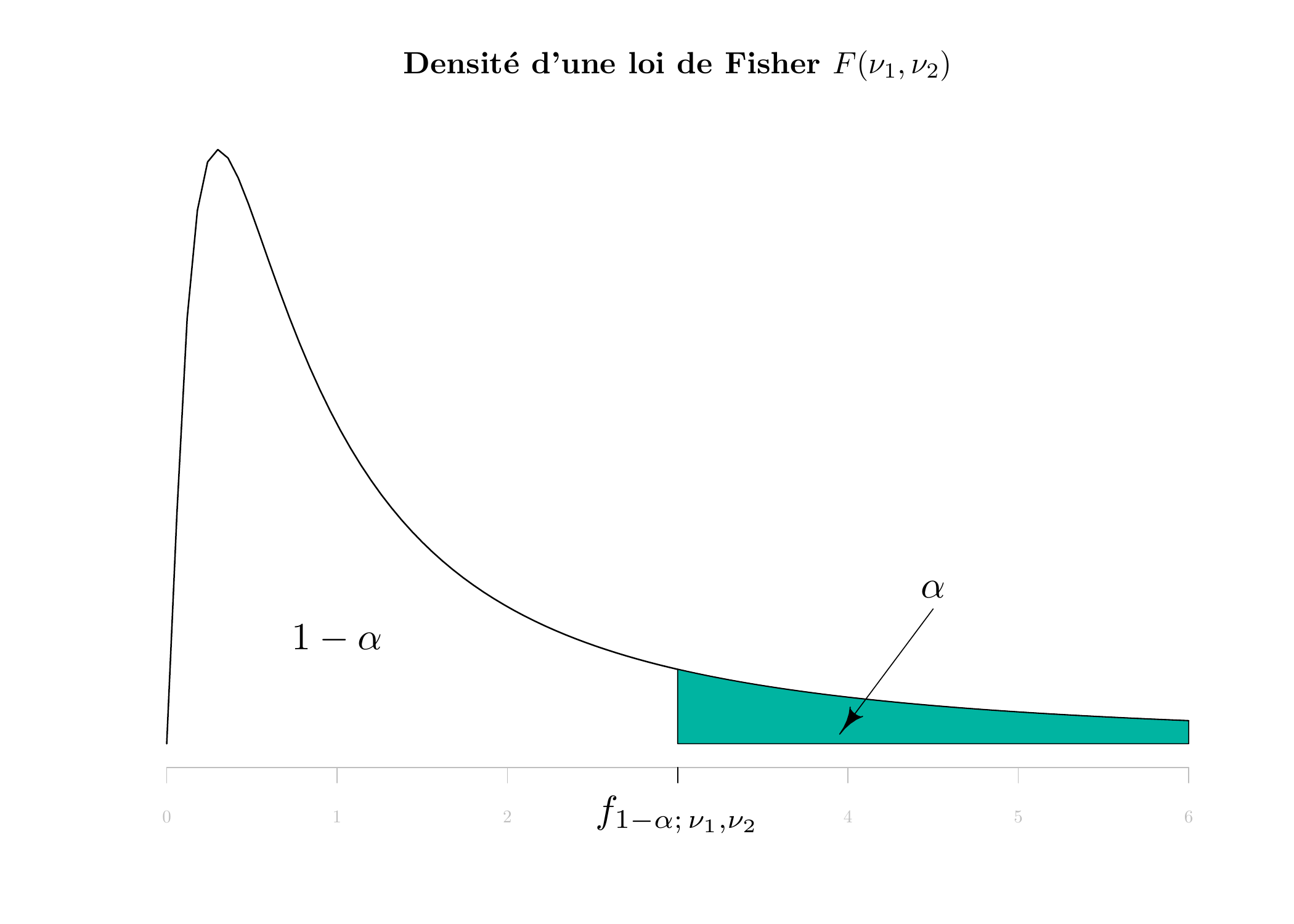
\(X\) étant une variable aléatoire de loi \(F(\nu_1,\nu_2)\) , les tables donnent les valeurs de \(f_{1-\alpha; \,\nu_1,\nu_2}= F_{F(\nu_1,\nu_2)}^{-1}(1-\alpha)\) telles que \(P(X< f_{1-\alpha; \,\nu_1,\nu_2})=1-\alpha\) pour \(\alpha = 5\%\) et \(\alpha =1\%\) . En qf(1-alpha, nu1, nu2).
Remarque : \(f_{\alpha; \, \nu_1,\nu_2} = \frac{1}{f_{1-\alpha; \, \nu_2,\nu_1}}\)
Pour \(\alpha = 5\%\)
\(\nu_2 \backslash \nu_1\)
1
2
3
4
5
6
7
8
9
10
12
16
20
24
40
60
100
\(+\infty\)
1
161.45
199.50
215.71
224.58
230.16
233.99
236.77
238.88
240.54
241.88
243.91
246.46
248.01
249.05
251.14
252.20
253.04
254.31
2
18.51
19.00
19.16
19.25
19.30
19.33
19.35
19.37
19.39
19.40
19.41
19.43
19.45
19.45
19.47
19.48
19.49
19.50
3
10.13
9.55
9.28
9.12
9.01
8.94
8.89
8.85
8.81
8.79
8.74
8.69
8.66
8.64
8.59
8.57
8.55
8.53
4
7.71
6.94
6.59
6.39
6.26
6.16
6.09
6.04
6.00
5.96
5.91
5.84
5.80
5.77
5.72
5.69
5.66
5.63
5
6.61
5.79
5.41
5.19
5.05
4.95
4.88
4.82
4.77
4.74
4.68
4.60
4.56
4.53
4.46
4.43
4.41
4.37
6
5.99
5.14
4.76
4.53
4.39
4.28
4.21
4.15
4.10
4.06
4.00
3.92
3.87
3.84
3.77
3.74
3.71
3.67
7
5.59
4.74
4.35
4.12
3.97
3.87
3.79
3.73
3.68
3.64
3.58
3.49
3.44
3.41
3.34
3.30
3.27
3.23
8
5.32
4.46
4.07
3.84
3.69
3.58
3.50
3.44
3.39
3.35
3.28
3.20
3.15
3.12
3.04
3.00
2.98
2.93
9
5.12
4.26
3.86
3.63
3.48
3.37
3.29
3.23
3.18
3.14
3.07
2.99
2.94
2.90
2.83
2.79
2.76
2.71
10
4.96
4.10
3.71
3.48
3.33
3.22
3.13
3.07
3.02
2.98
2.91
2.83
2.77
2.74
2.66
2.62
2.59
2.54
11
4.84
3.98
3.59
3.36
3.20
3.10
3.01
2.95
2.90
2.85
2.79
2.70
2.65
2.61
2.53
2.49
2.46
2.40
12
4.75
3.88
3.49
3.26
3.11
3.00
2.91
2.85
2.80
2.75
2.69
2.60
2.54
2.50
2.43
2.38
2.35
2.30
13
4.67
3.81
3.41
3.18
3.02
2.92
2.83
2.77
2.71
2.67
2.60
2.52
2.46
2.42
2.34
2.30
2.26
2.21
14
4.60
3.74
3.34
3.11
2.96
2.85
2.76
2.70
2.65
2.60
2.53
2.44
2.39
2.35
2.27
2.22
2.19
2.13
15
4.54
3.68
3.29
3.06
2.90
2.79
2.71
2.64
2.59
2.54
2.48
2.38
2.33
2.29
2.20
2.16
2.12
2.07
16
4.49
3.63
3.24
3.01
2.85
2.74
2.66
2.59
2.54
2.49
2.42
2.33
2.28
2.23
2.15
2.11
2.07
2.01
17
4.45
3.59
3.20
2.96
2.81
2.70
2.61
2.55
2.49
2.45
2.38
2.29
2.23
2.19
2.10
2.06
2.02
1.96
18
4.41
3.56
3.16
2.93
2.77
2.66
2.58
2.51
2.46
2.41
2.34
2.25
2.19
2.15
2.06
2.02
1.98
1.92
19
4.38
3.52
3.13
2.90
2.74
2.63
2.54
2.48
2.42
2.38
2.31
2.21
2.15
2.11
2.03
1.98
1.94
1.88
20
4.35
3.49
3.10
2.87
2.71
2.60
2.51
2.45
2.39
2.35
2.28
2.18
2.12
2.08
1.99
1.95
1.91
1.84
21
4.33
3.47
3.07
2.84
2.68
2.57
2.49
2.42
2.37
2.32
2.25
2.16
2.10
2.05
1.97
1.92
1.88
1.81
22
4.30
3.44
3.05
2.82
2.66
2.55
2.46
2.40
2.34
2.30
2.23
2.13
2.07
2.03
1.94
1.89
1.85
1.78
23
4.28
3.42
3.03
2.80
2.64
2.53
2.44
2.38
2.32
2.27
2.20
2.11
2.05
2.00
1.91
1.86
1.82
1.76
24
4.26
3.40
3.01
2.78
2.62
2.51
2.42
2.35
2.30
2.25
2.18
2.09
2.03
1.98
1.89
1.84
1.80
1.73
25
4.24
3.38
2.99
2.76
2.60
2.49
2.40
2.34
2.28
2.24
2.16
2.07
2.01
1.96
1.87
1.82
1.78
1.71
26
4.22
3.37
2.98
2.74
2.59
2.47
2.39
2.32
2.27
2.22
2.15
2.05
1.99
1.95
1.85
1.80
1.76
1.69
27
4.21
3.35
2.96
2.73
2.57
2.46
2.37
2.31
2.25
2.20
2.13
2.04
1.97
1.93
1.84
1.78
1.74
1.67
28
4.20
3.34
2.95
2.71
2.56
2.44
2.36
2.29
2.24
2.19
2.12
2.02
1.96
1.92
1.82
1.77
1.73
1.65
29
4.18
3.33
2.93
2.70
2.54
2.43
2.35
2.28
2.22
2.18
2.10
2.01
1.95
1.90
1.81
1.75
1.71
1.64
30
4.17
3.32
2.92
2.69
2.53
2.42
2.33
2.27
2.21
2.16
2.09
2.00
1.93
1.89
1.79
1.74
1.70
1.62
40
4.08
3.23
2.84
2.61
2.45
2.34
2.25
2.18
2.12
2.08
2.00
1.90
1.84
1.79
1.69
1.64
1.59
1.51
50
4.03
3.18
2.79
2.56
2.40
2.29
2.20
2.13
2.07
2.03
1.95
1.85
1.78
1.74
1.63
1.58
1.52
1.44
60
4.00
3.15
2.76
2.52
2.37
2.25
2.17
2.10
2.04
1.99
1.92
1.81
1.75
1.70
1.59
1.53
1.48
1.39
100
3.94
3.09
2.70
2.46
2.31
2.19
2.10
2.03
1.98
1.93
1.85
1.75
1.68
1.63
1.51
1.45
1.39
1.28
\(+\infty\)
3.84
3.00
2.60
2.37
2.21
2.10
2.01
1.94
1.88
1.83
1.75
1.64
1.57
1.52
1.39
1.32
1.24
1.00
Pour \(\alpha = 2.5\%\)
\(\nu_2 \backslash \nu_1\)
1
2
3
4
5
6
7
8
9
10
12
16
20
24
40
60
100
\(+\infty\)
1
647.79
799.50
864.16
899.58
921.85
937.11
948.22
956.66
963.28
968.63
976.71
986.92
993.10
997.25
1005.60
1009.80
1013.17
1018.26
2
38.51
39.00
39.16
39.25
39.30
39.33
39.35
39.37
39.39
39.40
39.41
39.44
39.45
39.46
39.47
39.48
39.49
39.50
3
17.44
16.04
15.44
15.10
14.88
14.73
14.62
14.54
14.47
14.42
14.34
14.23
14.17
14.12
14.04
13.99
13.96
13.90
4
12.22
10.65
9.98
9.61
9.36
9.20
9.07
8.98
8.90
8.84
8.75
8.63
8.56
8.51
8.41
8.36
8.32
8.26
5
10.01
8.43
7.76
7.39
7.15
6.98
6.85
6.76
6.68
6.62
6.53
6.40
6.33
6.28
6.17
6.12
6.08
6.01
6
8.81
7.26
6.60
6.23
5.99
5.82
5.70
5.60
5.52
5.46
5.37
5.24
5.17
5.12
5.01
4.96
4.92
4.85
7
8.07
6.54
5.89
5.52
5.29
5.12
5.00
4.90
4.82
4.76
4.67
4.54
4.47
4.42
4.31
4.25
4.21
4.14
8
7.57
6.06
5.42
5.05
4.82
4.65
4.53
4.43
4.36
4.29
4.20
4.08
4.00
3.95
3.84
3.78
3.74
3.67
9
7.21
5.71
5.08
4.72
4.48
4.32
4.20
4.10
4.03
3.96
3.87
3.74
3.67
3.61
3.50
3.45
3.40
3.33
10
6.94
5.46
4.83
4.47
4.24
4.07
3.95
3.85
3.78
3.72
3.62
3.50
3.42
3.37
3.25
3.20
3.15
3.08
11
6.72
5.26
4.63
4.28
4.04
3.88
3.76
3.66
3.59
3.53
3.43
3.30
3.23
3.17
3.06
3.00
2.96
2.88
12
6.55
5.10
4.47
4.12
3.89
3.73
3.61
3.51
3.44
3.37
3.28
3.15
3.07
3.02
2.91
2.85
2.80
2.73
13
6.41
4.96
4.35
4.00
3.77
3.60
3.48
3.39
3.31
3.25
3.15
3.03
2.95
2.89
2.78
2.72
2.67
2.60
14
6.30
4.86
4.24
3.89
3.66
3.50
3.38
3.29
3.21
3.15
3.05
2.92
2.84
2.79
2.67
2.61
2.56
2.49
15
6.20
4.76
4.15
3.80
3.58
3.42
3.29
3.20
3.12
3.06
2.96
2.84
2.76
2.70
2.58
2.52
2.47
2.40
16
6.12
4.69
4.08
3.73
3.50
3.34
3.22
3.12
3.05
2.99
2.89
2.76
2.68
2.62
2.51
2.45
2.40
2.32
17
6.04
4.62
4.01
3.66
3.44
3.28
3.16
3.06
2.98
2.92
2.83
2.70
2.62
2.56
2.44
2.38
2.33
2.25
18
5.98
4.56
3.95
3.61
3.38
3.22
3.10
3.00
2.93
2.87
2.77
2.64
2.56
2.50
2.38
2.32
2.27
2.19
19
5.92
4.51
3.90
3.56
3.33
3.17
3.05
2.96
2.88
2.82
2.72
2.59
2.51
2.45
2.33
2.27
2.22
2.13
20
5.87
4.46
3.86
3.52
3.29
3.13
3.01
2.91
2.84
2.77
2.68
2.55
2.46
2.41
2.29
2.22
2.17
2.08
21
5.83
4.42
3.82
3.48
3.25
3.09
2.97
2.87
2.80
2.73
2.64
2.51
2.42
2.37
2.25
2.18
2.13
2.04
22
5.79
4.38
3.78
3.44
3.21
3.06
2.93
2.84
2.76
2.70
2.60
2.47
2.39
2.33
2.21
2.14
2.09
2.00
23
5.75
4.35
3.75
3.41
3.18
3.02
2.90
2.81
2.73
2.67
2.57
2.44
2.36
2.30
2.18
2.11
2.06
1.97
24
5.72
4.32
3.72
3.38
3.15
3.00
2.87
2.78
2.70
2.64
2.54
2.41
2.33
2.27
2.15
2.08
2.02
1.94
25
5.69
4.29
3.69
3.35
3.13
2.97
2.85
2.75
2.68
2.61
2.52
2.38
2.30
2.24
2.12
2.05
2.00
1.91
26
5.66
4.26
3.67
3.33
3.10
2.94
2.82
2.73
2.65
2.59
2.49
2.36
2.28
2.22
2.09
2.03
1.97
1.88
27
5.63
4.24
3.65
3.31
3.08
2.92
2.80
2.71
2.63
2.57
2.47
2.34
2.25
2.19
2.07
2.00
1.95
1.85
28
5.61
4.22
3.63
3.29
3.06
2.90
2.78
2.69
2.61
2.55
2.45
2.32
2.23
2.17
2.05
1.98
1.92
1.83
29
5.59
4.20
3.61
3.27
3.04
2.88
2.76
2.67
2.59
2.53
2.43
2.30
2.21
2.15
2.03
1.96
1.90
1.81
30
5.57
4.18
3.59
3.25
3.03
2.87
2.75
2.65
2.58
2.51
2.41
2.28
2.19
2.14
2.01
1.94
1.88
1.79
40
5.42
4.05
3.46
3.13
2.90
2.74
2.62
2.53
2.45
2.39
2.29
2.15
2.07
2.01
1.88
1.80
1.74
1.64
50
5.34
3.98
3.39
3.05
2.83
2.67
2.55
2.46
2.38
2.32
2.22
2.08
1.99
1.93
1.80
1.72
1.66
1.54
60
5.29
3.92
3.34
3.01
2.79
2.63
2.51
2.41
2.33
2.27
2.17
2.03
1.94
1.88
1.74
1.67
1.60
1.48
100
5.18
3.83
3.25
2.92
2.70
2.54
2.42
2.32
2.24
2.18
2.08
1.94
1.85
1.78
1.64
1.56
1.48
1.35
\(+\infty\)
5.02
3.69
3.12
2.79
2.57
2.41
2.29
2.19
2.11
2.05
1.95
1.80
1.71
1.64
1.48
1.39
1.30
1.00
Pour \(\alpha = 1\%\)
\(\nu_2 \backslash \nu_1\)
1
2
3
4
5
6
7
8
9
10
12
16
20
24
40
60
100
\(+\infty\)
1
4052.18
4999.50
5403.35
5624.58
5763.65
5858.99
5928.36
5981.07
6022.47
6055.85
6106.32
6170.10
6208.73
6234.63
6286.78
6313.03
6334.11
6365.86
2
98.50
99.00
99.17
99.25
99.30
99.33
99.36
99.37
99.39
99.40
99.42
99.44
99.45
99.46
99.47
99.48
99.49
99.50
3
34.12
30.82
29.46
28.71
28.24
27.91
27.67
27.49
27.34
27.23
27.05
26.83
26.69
26.60
26.41
26.32
26.24
26.12
4
21.20
18.00
16.69
15.98
15.52
15.21
14.98
14.80
14.66
14.55
14.37
14.15
14.02
13.93
13.74
13.65
13.58
13.46
5
16.26
13.27
12.06
11.39
10.97
10.67
10.46
10.29
10.16
10.05
9.89
9.68
9.55
9.47
9.29
9.20
9.13
9.02
6
13.74
10.93
9.78
9.15
8.75
8.47
8.26
8.10
7.98
7.87
7.72
7.52
7.40
7.31
7.14
7.06
6.99
6.88
7
12.25
9.55
8.45
7.85
7.46
7.19
6.99
6.84
6.72
6.62
6.47
6.28
6.16
6.07
5.91
5.82
5.75
5.65
8
11.26
8.65
7.59
7.01
6.63
6.37
6.18
6.03
5.91
5.81
5.67
5.48
5.36
5.28
5.12
5.03
4.96
4.86
9
10.56
8.02
6.99
6.42
6.06
5.80
5.61
5.47
5.35
5.26
5.11
4.92
4.81
4.73
4.57
4.48
4.42
4.31
10
10.04
7.56
6.55
5.99
5.64
5.39
5.20
5.06
4.94
4.85
4.71
4.52
4.41
4.33
4.16
4.08
4.01
3.91
11
9.65
7.21
6.22
5.67
5.32
5.07
4.89
4.74
4.63
4.54
4.40
4.21
4.10
4.02
3.86
3.78
3.71
3.60
12
9.33
6.93
5.95
5.41
5.06
4.82
4.64
4.50
4.39
4.30
4.16
3.97
3.86
3.78
3.62
3.54
3.47
3.36
13
9.07
6.70
5.74
5.21
4.86
4.62
4.44
4.30
4.19
4.10
3.96
3.78
3.66
3.59
3.42
3.34
3.27
3.16
14
8.86
6.51
5.56
5.04
4.70
4.46
4.28
4.14
4.03
3.94
3.80
3.62
3.50
3.43
3.27
3.18
3.11
3.00
15
8.68
6.36
5.42
4.89
4.56
4.32
4.14
4.00
3.90
3.81
3.67
3.48
3.37
3.29
3.13
3.05
2.98
2.87
16
8.53
6.23
5.29
4.77
4.44
4.20
4.03
3.89
3.78
3.69
3.55
3.37
3.26
3.18
3.02
2.93
2.86
2.75
17
8.40
6.11
5.18
4.67
4.34
4.10
3.93
3.79
3.68
3.59
3.46
3.27
3.16
3.08
2.92
2.83
2.76
2.65
18
8.29
6.01
5.09
4.58
4.25
4.01
3.84
3.71
3.60
3.51
3.37
3.19
3.08
3.00
2.83
2.75
2.68
2.57
19
8.19
5.93
5.01
4.50
4.17
3.94
3.77
3.63
3.52
3.43
3.30
3.12
3.00
2.92
2.76
2.67
2.60
2.49
20
8.10
5.85
4.94
4.43
4.10
3.87
3.70
3.56
3.46
3.37
3.23
3.05
2.94
2.86
2.69
2.61
2.54
2.42
21
8.02
5.78
4.87
4.37
4.04
3.81
3.64
3.51
3.40
3.31
3.17
2.99
2.88
2.80
2.64
2.55
2.48
2.36
22
7.95
5.72
4.82
4.31
3.99
3.76
3.59
3.45
3.35
3.26
3.12
2.94
2.83
2.75
2.58
2.50
2.42
2.31
23
7.88
5.66
4.76
4.26
3.94
3.71
3.54
3.41
3.30
3.21
3.07
2.89
2.78
2.70
2.54
2.45
2.37
2.26
24
7.82
5.61
4.72
4.22
3.90
3.67
3.50
3.36
3.26
3.17
3.03
2.85
2.74
2.66
2.49
2.40
2.33
2.21
25
7.77
5.57
4.67
4.18
3.85
3.63
3.46
3.32
3.22
3.13
2.99
2.81
2.70
2.62
2.45
2.36
2.29
2.17
26
7.72
5.53
4.64
4.14
3.82
3.59
3.42
3.29
3.18
3.09
2.96
2.78
2.66
2.58
2.42
2.33
2.25
2.13
27
7.68
5.49
4.60
4.11
3.79
3.56
3.39
3.26
3.15
3.06
2.93
2.75
2.63
2.55
2.38
2.29
2.22
2.10
28
7.64
5.45
4.57
4.07
3.75
3.53
3.36
3.23
3.12
3.03
2.90
2.72
2.60
2.52
2.35
2.26
2.19
2.06
29
7.60
5.42
4.54
4.04
3.73
3.50
3.33
3.20
3.09
3.00
2.87
2.69
2.57
2.50
2.33
2.23
2.16
2.03
30
7.56
5.39
4.51
4.02
3.70
3.47
3.30
3.17
3.07
2.98
2.84
2.66
2.55
2.47
2.30
2.21
2.13
2.01
40
7.31
5.18
4.31
3.83
3.51
3.29
3.12
2.99
2.89
2.80
2.66
2.48
2.37
2.29
2.11
2.02
1.94
1.80
50
7.17
5.06
4.20
3.72
3.41
3.19
3.02
2.89
2.79
2.70
2.56
2.38
2.27
2.18
2.01
1.91
1.82
1.68
60
7.08
4.98
4.13
3.65
3.34
3.12
2.95
2.82
2.72
2.63
2.50
2.31
2.20
2.12
1.94
1.84
1.75
1.60
100
6.89
4.82
3.98
3.51
3.21
2.99
2.82
2.69
2.59
2.50
2.37
2.18
2.07
1.98
1.80
1.69
1.60
1.43
\(+\infty\)
6.63
4.61
3.78
3.32
3.02
2.80
2.64
2.51
2.41
2.32
2.18
2.00
1.88
1.79
1.59
1.47
1.36
1.00
Pour \(\alpha = 0.05\%\)
\(\nu_2 \backslash \nu_1\)
1
2
3
4
5
6
7
8
9
10
12
16
20
24
40
60
100
\(+\infty\)
1
161.45
199.50
215.71
224.58
230.16
233.99
236.77
238.88
240.54
241.88
243.91
246.46
248.01
249.05
251.14
252.20
253.04
254.31
2
18.51
19.00
19.16
19.25
19.30
19.33
19.35
19.37
19.39
19.40
19.41
19.43
19.45
19.45
19.47
19.48
19.49
19.50
3
10.13
9.55
9.28
9.12
9.01
8.94
8.89
8.85
8.81
8.79
8.74
8.69
8.66
8.64
8.59
8.57
8.55
8.53
4
7.71
6.94
6.59
6.39
6.26
6.16
6.09
6.04
6.00
5.96
5.91
5.84
5.80
5.77
5.72
5.69
5.66
5.63
5
6.61
5.79
5.41
5.19
5.05
4.95
4.88
4.82
4.77
4.74
4.68
4.60
4.56
4.53
4.46
4.43
4.41
4.37
6
5.99
5.14
4.76
4.53
4.39
4.28
4.21
4.15
4.10
4.06
4.00
3.92
3.87
3.84
3.77
3.74
3.71
3.67
7
5.59
4.74
4.35
4.12
3.97
3.87
3.79
3.73
3.68
3.64
3.58
3.49
3.44
3.41
3.34
3.30
3.27
3.23
8
5.32
4.46
4.07
3.84
3.69
3.58
3.50
3.44
3.39
3.35
3.28
3.20
3.15
3.12
3.04
3.00
2.98
2.93
9
5.12
4.26
3.86
3.63
3.48
3.37
3.29
3.23
3.18
3.14
3.07
2.99
2.94
2.90
2.83
2.79
2.76
2.71
10
4.96
4.10
3.71
3.48
3.33
3.22
3.13
3.07
3.02
2.98
2.91
2.83
2.77
2.74
2.66
2.62
2.59
2.54
11
4.84
3.98
3.59
3.36
3.20
3.10
3.01
2.95
2.90
2.85
2.79
2.70
2.65
2.61
2.53
2.49
2.46
2.40
12
4.75
3.88
3.49
3.26
3.11
3.00
2.91
2.85
2.80
2.75
2.69
2.60
2.54
2.50
2.43
2.38
2.35
2.30
13
4.67
3.81
3.41
3.18
3.02
2.92
2.83
2.77
2.71
2.67
2.60
2.52
2.46
2.42
2.34
2.30
2.26
2.21
14
4.60
3.74
3.34
3.11
2.96
2.85
2.76
2.70
2.65
2.60
2.53
2.44
2.39
2.35
2.27
2.22
2.19
2.13
15
4.54
3.68
3.29
3.06
2.90
2.79
2.71
2.64
2.59
2.54
2.48
2.38
2.33
2.29
2.20
2.16
2.12
2.07
16
4.49
3.63
3.24
3.01
2.85
2.74
2.66
2.59
2.54
2.49
2.42
2.33
2.28
2.23
2.15
2.11
2.07
2.01
17
4.45
3.59
3.20
2.96
2.81
2.70
2.61
2.55
2.49
2.45
2.38
2.29
2.23
2.19
2.10
2.06
2.02
1.96
18
4.41
3.56
3.16
2.93
2.77
2.66
2.58
2.51
2.46
2.41
2.34
2.25
2.19
2.15
2.06
2.02
1.98
1.92
19
4.38
3.52
3.13
2.90
2.74
2.63
2.54
2.48
2.42
2.38
2.31
2.21
2.15
2.11
2.03
1.98
1.94
1.88
20
4.35
3.49
3.10
2.87
2.71
2.60
2.51
2.45
2.39
2.35
2.28
2.18
2.12
2.08
1.99
1.95
1.91
1.84
21
4.33
3.47
3.07
2.84
2.68
2.57
2.49
2.42
2.37
2.32
2.25
2.16
2.10
2.05
1.97
1.92
1.88
1.81
22
4.30
3.44
3.05
2.82
2.66
2.55
2.46
2.40
2.34
2.30
2.23
2.13
2.07
2.03
1.94
1.89
1.85
1.78
23
4.28
3.42
3.03
2.80
2.64
2.53
2.44
2.38
2.32
2.27
2.20
2.11
2.05
2.00
1.91
1.86
1.82
1.76
24
4.26
3.40
3.01
2.78
2.62
2.51
2.42
2.35
2.30
2.25
2.18
2.09
2.03
1.98
1.89
1.84
1.80
1.73
25
4.24
3.38
2.99
2.76
2.60
2.49
2.40
2.34
2.28
2.24
2.16
2.07
2.01
1.96
1.87
1.82
1.78
1.71
26
4.22
3.37
2.98
2.74
2.59
2.47
2.39
2.32
2.27
2.22
2.15
2.05
1.99
1.95
1.85
1.80
1.76
1.69
27
4.21
3.35
2.96
2.73
2.57
2.46
2.37
2.31
2.25
2.20
2.13
2.04
1.97
1.93
1.84
1.78
1.74
1.67
28
4.20
3.34
2.95
2.71
2.56
2.44
2.36
2.29
2.24
2.19
2.12
2.02
1.96
1.92
1.82
1.77
1.73
1.65
29
4.18
3.33
2.93
2.70
2.54
2.43
2.35
2.28
2.22
2.18
2.10
2.01
1.95
1.90
1.81
1.75
1.71
1.64
30
4.17
3.32
2.92
2.69
2.53
2.42
2.33
2.27
2.21
2.16
2.09
2.00
1.93
1.89
1.79
1.74
1.70
1.62
40
4.08
3.23
2.84
2.61
2.45
2.34
2.25
2.18
2.12
2.08
2.00
1.90
1.84
1.79
1.69
1.64
1.59
1.51
50
4.03
3.18
2.79
2.56
2.40
2.29
2.20
2.13
2.07
2.03
1.95
1.85
1.78
1.74
1.63
1.58
1.52
1.44
60
4.00
3.15
2.76
2.52
2.37
2.25
2.17
2.10
2.04
1.99
1.92
1.81
1.75
1.70
1.59
1.53
1.48
1.39
100
3.94
3.09
2.70
2.46
2.31
2.19
2.10
2.03
1.98
1.93
1.85
1.75
1.68
1.63
1.51
1.45
1.39
1.28
\(+\infty\)
3.84
3.00
2.60
2.37
2.21
2.10
2.01
1.94
1.88
1.83
1.75
1.64
1.57
1.52
1.39
1.32
1.24
1.00