1 Variables Aléatoires Discrètes

Notion de variable aléatoire réelle (v.a.r.)

Après avoir réalisé une expérience aléatoire, il arrive bien souvent qu’on s’intéresse plus à une fonction du résultat qu’au résultat lui-même. Expliquons ceci au moyen des exemples suivants: lorsqu’on joue au dés, certains jeux accordent de l’importance à la somme obtenue sur deux dés, 7 par exemple, plutôt qu’à la question de savoir si c’est la paire (1,6) qui est apparue, ou (2,5), (3,4), (4,3), (5,2) ou plutôt (6,1). Dans le cas du jet d’une pièce, il peut être plus intéressant de connaître le nombre de fois où le côté pile est apparue plutôt que la séquence détaillée des jets pile et face. Ces grandeurs auxquelles on s’intéresse sont en fait des fonctions réelles définies sur l’ensemble fondamental et sont appelées variables aléatoires.

Du fait que la valeur d’une variable aléatoire est déterminée par le résultat de l’expérience, il est possible d’attribuer une probabilité aux différentes valeurs que la variable aléatoire peut prendre.

Soient \(\varepsilon\) une expérience aléatoire et \((\Omega,\mathcal{A},P)\) un espace probabilisé lié à cette expérience. Dans de nombreuses situations, on associe à chaque résultat \(\omega \in \Omega\) un nombre réel noté \(X(\omega)\); on construit ainsi une application \(X : \Omega \rightarrow \mathbb{R}\). Historiquement, \(\varepsilon\) était un jeu et \(X\) représentait le gain du joueur.

Exemple: Un joueur lance un dé équilibré à 6 faces numérotées de 1 à 6, et on observe le numéro obtenu.

• Si le joueur obtient 1, 3 ou 5, il gagne 1 euro.

• S’il obtient 2 ou 4, il gagne 5 euros.

• S’il obtient 6, il perd 10 euros.

Selon l’expérience aléatoire (lancer d’un dé équilibré) l’ensemble fondamental est \(\Omega = \{1,2,3,4,5,6\}\), \(\mathcal{A} = \mathcal{P}(\Omega)\) et \(P\) l’équiprobabilité sur \((\Omega,\mathcal{A})\). Soit \(X\) l’application de \(\Omega\) dans \(\mathbb{R}\) qui à tout \(\omega \in \Omega\) associe le gain correspondant. On a donc

• \(X(1) = X(3) = X(5) = 1\)

• \(X(2) = X(4) = 5\)

• \(X(6) = -10\)

On dit que \(X\) est une variable aléatoire sur \(\Omega\).

On peut s’intéresser à la probabilité de gagner 1 euro, c’est-à-dire d’avoir \(X(\omega) = 1\), ce qui se réalise si et seulement si \(\omega \in \{1,3,5\}\). La probabilité cherchée est donc égale à \(P(\{1,3,5\}) = 1/2\). On écrira aussi \(P(X=1) = 1/2\).

On pourra donc considérer l’événement : \[\{X=1\} = \{\omega \in \Omega / X(\omega) = 1\} = \{\omega \in \Omega / X(\omega) \in \{1\}\} = X^{-1} (\{1\}) = \{1,3,5\}.\]

On aura du même \(P(X=5) = 1/3\) et \(P(X=-10) = 1/6\). Ce que l’on peut présenter dans un tableau

\(x_i\)	-10	1	5
\(p_i=P(X = x_i)\)	\(1/6\)	\(1/2\)	\(1/3\)

Cela revient à considérer un nouvel ensemble d’événements élémentaires: \[\Omega_X = X(\Omega)= \{-10,1,5\}\] et à munir cet ensemble de la probabilité \(P_X\) définie par le tableau des \(P(X=x_i)\) ci dessus. Cette nouvelle probabilité s’appelle loi de la variable aléatoire X.

Remarquer que \[P(\bigcup_{x_i \in \Omega_X} \{X=x_i\}) = \sum_{x_i \in \Omega_X} P(X=x_i) = 1\]

Dans ce chapitre, nous traitons le cas où \(X(\Omega)\) est dénombrable. La variable aléatoire est alors dite discrète. Sa loi de probabilité, qui peut être toujours définie par sa fonction de répartition, le sera plutôt par les probabilités individuelles. Nous définirons les deux caractéristiques numériques principales d’une variable aléatoire discrète, l’espérance caractéristique de valeur centrale, et la variance, caractéristique de dispersion. Nous définirons aussi les couples de variables aléatoires.

Définition, loi de probabilité

Définition 1.1 On dit qu’une variable aléatoire réelle (v.a.r.) \(X\) est discrète (v.a.r.d.) si l’ensemble des valeurs que prend \(X\) est fini ou infini dénombrable.

Si on suppose \(X(\Omega)\) l’ensemble des valeurs de \(X\) qui admet un plus petit élément \(x_1\). Alors la v.a.r.d. \(X\) est entièrement définie par:

• L’ensemble \(X(\Omega)\) des valeurs prises par \(X\), rangées par ordre croissant: \(X(\Omega) = \{x_1, x_2,\ldots,x_i,\ldots\}\) avec \(x_1 \leq x_2 \leq \ldots \leq x_i \leq \ldots\).

• La loi de probabilité définie sur \(X(\Omega)\) par \[p_i = P(X=x_i) \,\,\,\,\, \forall \,\, i=1,2,\ldots\]

Remarques:

• Soit \(B\) un ensemble de \(\mathbb{R}\), \[P(X \in B) = \sum_{i / x_i \in B} p(x_i)\]

• En particulier \[P( a < X \leq b) = \sum_{i / a < x_i \leq b} p(x_i)\]

• Bien sûr tous les \(p(x_i)\) sont positives et \(\sum_{i=1}^{\infty} p(x_i) =1\).

• Si \(X\) ne prend qu’un petit nombre de valeurs, cette loi est généralement présentée dans un tableau.

Fonction de répartition d’une variable aléatoire discrète

Définition 1.2 On appelle fonction de répartition de la v.a. \(X\), qu’on note \(F(a)\) de la v.a.r.d. \(X\), ou \(F_X(a)\), la fonction définie pour tout réel \(a\), \(-\infty < a < \infty\), par

\[F(a)=P(X \leq a)=\sum_{i / x_{i}\leq a} P(X=x_{i})\]

Cette valeur représente la probabilité de toutes les réalisations inférieures ou égales au réel \(a\).

Propriétés: Voici quelques propriétés de cette fonction:

1. C’est une fonction en escalier (constante par morceaux).

2. \(F(a) \leq 1\) car c’est une probabilité.

3. \(F(a)\) est continue à droite.

4. \(\lim\limits_{a\to - \infty} F(a) = 0\) et \(\lim\limits_{a\to\infty} F(a) = 1\)

La fonction de répartition caractérise la loi de \(X\), autrement dit: \(F_{X} = F_{Y}\) si et seulement si les variables aléatoires \(X\) et \(Y\) ont la même loi de probabilité.

Fonction de répartition et probabilités sur \(X\)

Tous les calculs de probabilité concernant \(X\) peuvent être traités en termes de fonction de répartition. Par exemple,

\[P(a < X \leq b) = F(b) - F(a) \quad \quad \text{pour tout } a < b\]

On peut mieux s’en rendre compte en écrivant \(\{X \leq b\}\) comme union des deux événements incompatibles \(\{X \leq a\}\) et \(\{ a < X \leq b\}\), soit

\[\{X \leq b\} = \{X \leq a\} \cup \{ a < X \leq b\}\]

et ainsi

\[P(X \leq b) = P(X \leq a) + P(a < X \leq b)\] ce qui établit l’égalité ci dessus.

On peut déduire de \(F\) les probabilités individuelles par:

\[p_{i}=F(x_{i})-F(x_{i-1})\quad \quad \text{pour } 1 \leq i \leq n\]

Exemple: On joue trois fois à pile ou face. Soit \(X\) la variable aléatoire “nombre de pile obtenus”. Ici \(\Omega=\{P, F\}^3\), et donc \[X(\Omega)=\{0, 1, 2, 3\}.\]

On a \(card(\Omega)=2^3=8\). Calculons par exemple \(P(X=1)\), c’est à dire la probabilité d’avoir exactement une pile. \[X^{-1}(1)=\{(P, F, F), (F, P, F), (F, F, P) \}\] D’où \(P(X=1)=\frac{3}{8}\).

En procédant de la même façon, on obtient la loi de probabilité de \(X\):

\(k\)	0	1	2	3
\(P(X = k)\)	\(\frac{1}{8}\)	\(\frac{3}{8}\)	\(\frac{3}{8}\)	\(\frac{1}{8}\)

La fonction de répartition de \(X\) est donc donnée par:

\[F(x) = \left\{ \begin{array}{l l} 0 & \quad \text{si $x<0$}\\ 1/8 & \quad \text{si $0 \leq x < 1$}\\ 1/2 & \quad \text{si $1 \leq x < 2$}\\ 7/8 & \quad \text{si $2 \leq x < 3$}\\ 1 & \quad \text{si $x \geq 3$}\\ \end{array} \right.\]

Le graphe de cette dernière est représentée dans la figure suivante:

## 
## Attaching package: 'latex2exp'
## The following object is masked from 'package:plotly':
## 
##     TeX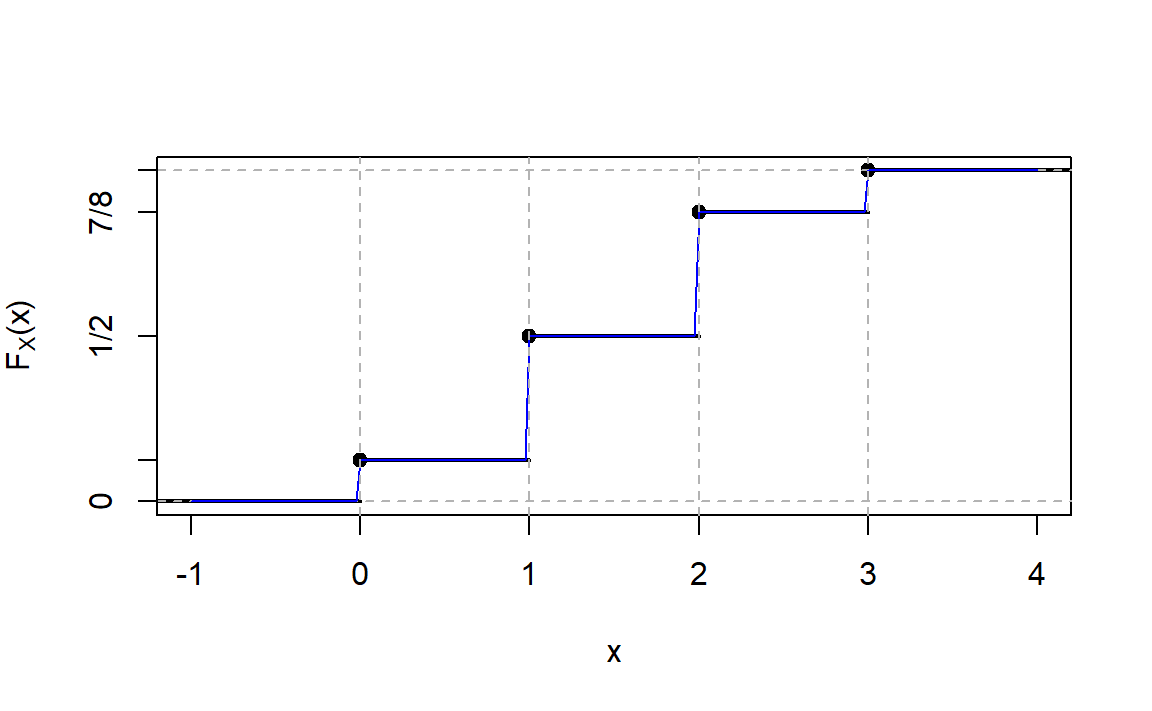

Exemple: Soit \(A\) un événement quelconque. On appelle variable aléatoire indicatrice de cet événement \(A\), la variable aléatoire définie par: \[X(\omega) = \left\{ \begin{array}{l l} 1 & \quad \text{si $\omega \in A$}\\ 0 & \quad \text{si $\omega \in \bar{A}$}\\ \end{array} \right.\]

et notée \(X=1_A\). Ainsi: \[P(X=1)=P(A)=p\] \[P(X=0)=P(\bar{A})=1-p\]

La fonction de répartition de \(X\) est donc donnée par:

\[F(x) = \left\{ \begin{array}{l l} 0 & \quad \text{si $x<0$}\\ 1-p & \quad \text{si $0 \leq x < 1$}\\ 1 & \quad \text{si $x \geq 1$}\\ \end{array} \right.\]

On peut prendre par exemple le cas d’un tirage d’une boule dans une urne contenant 2 boules blanches et 3 boules noires. Soit \(A:\text{"obtenir une boule blanche"}\) et \(X\) la variable indicatrice de \(A\). La loi de probabilité de \(X\) est alors

\(k\)	0	1
\(P(X = k)\)	\(\frac{3}{5}\)	\(\frac{2}{5}\)

et sa fonction de répartition est:

\[F(x) = \left\{ \begin{array}{l l} 0 & \quad \text{si $x<0$}\\ 3/5 & \quad \text{si $0 \leq x < 1$}\\ 1 & \quad \text{si $x \geq 1$}\\ \end{array} \right.\]

Moments d’une variable aléatoire discrète

Espérance mathématique

Définition 1.3 Pour une variable aléatoire discrète \(X\) de loi de probabilité \(p(.)\), on définit l’espérance de \(X\), notée \(E(X)\), par l’expression

\[E(X)=\sum_{i \in \mathbb{N}} x_{i} p(x_i)\]

En termes concrets, l’espérance de \(X\) est la moyenne pondérée des valeurs que \(X\) peut prendre, les poids étant les probabilités que ces valeurs soient prises.

Reprenons l’exemple où on joue 3 fois à pile ou face. L’espérance de \(X=\)“nombre de pile obtenus” est égal à: \[E(X)=0 \times \frac{1}{8}+1 \times \frac{3}{8}+2 \times \frac{3}{8}+3 \times \frac{1}{8}=1.5\]

Dans le cas de la loi uniforme sur \(X(\Omega)=\{x_{1},\ldots, x_{k}\}\), c’est à dire avec équiprobabilité de toutes les valeurs \(p_{i}=1/k\), on obtient: \[E(X)=\frac{1}{k} \sum_{i=1}^k x_{i}\] et dans ce cas \(E(X)\) se confond avec la moyenne arithmétique simple \(\bar{x}\) des valeurs possibles de \(X\).

Pour le jet d’un dé équilibré par exemple: \[E(X)=\frac{1}{6} \sum_{i=1}^6 i=\frac{7}{2}=3.5\]

Espérance d’une fonction d’une variable aléatoire

Théorème 1.1 (Théorème du transfert) Si X est une variable aléatoire discrète pouvant prendre ses valeurs parmi les valeurs \(x_i\), \(i \geq 1\), avec des probabilités respectives \(p(x_i)\), alors pour toute fonction réelle \(g\) on a

\[E(g(X)) = \sum_i g(x_i)p(x_i)\]

Exemple1.1 Soit \(X\) une variable aléatoire qui prend une des trois valeurs \(\{-1,0,1\}\) avec les probabilités respectives

\[P(X=-1) = 0.2 \quad \quad P(X=0)=0.5 \quad \quad P(X=1) = 0.3\]

Calculer \(E(X^2)\).

Solution: Première approche: Soit \(Y=X^2\). La distribution de \(Y\) est donnée par \[\begin{aligned} P(Y=1) &= P(X=-1) + P(X=1) = 0.5 \\ P(Y=0) &= P(X=0) = 0.5 \end{aligned}\] Donc \[E(X^2)=E(Y) = 1(0.5) + 0(0.5) = 0.5\]

Deuxième approche: En utilisant le théorème

\[\begin{aligned} E(X^2) &= (-1)^2(0.2) + 0^2(0.5) + 1^2 (0.3) \\ &= 1(0.2+0.3)+0(0.5)=0.5 \end{aligned}\]

Remarquer que \[0.5=E(X^2) \neq (E(X))^2 = 0.01\]

Linéarité de l’espérance Propriétés de l’espérance

1. \(E(X+a)=E(X)+a, \quad a \in \mathbb{R}\)
   résultat qui se déduit de: \[\sum_{i}p_{i}(x_{i}+a)= \sum_{i}p_{i}x_{i}+\sum_{i}ap_{i}=\sum_{i}p_{i}x_{i}+a \sum_{i}p_{i}=\sum_{i}p_{i}x_{i}+a\]

2. \(E(aX)=aE(X), \quad a\in \mathbb{R}\)
   il suffit d’écrire: \[\sum_{i}p_{i}a x_{i}=a\sum_{i}p_{i}x_{i}\]

3. \(E(X+Y)=E(X)+E(Y)\), \(X\) et \(Y\) étant deux variables aléatoire.

On peut résumer ces trois propriétés en disant que l’espérance mathématique est linéaire: \[E(\lambda X + \mu Y)= \lambda E(X)+\mu E(Y), \quad \forall \lambda \in \mathbb{R}, \, \forall \mu \in \mathbb{R}.\]

Variance

Définition 1.4 La variance est un indicateur mesurant la dispersion des valeurs \(x_{i}\) que peut prendre la v.a. \(X\) et son espérance \(E(X)\). On appelle variance de X, que l’on note \(V(X)\), la quantité

\[V(X)=E\big[ (X-E(X))^2 \big]\] lorsque cette quantité existe.
C’est l’espérance mathématique du carré de la v.a. centrée \(X-E(X)\).

On peut établir une autre formule pour le calcul de \(V(X)\):

\[V(X)=E(X^2)-E^2(X)\]

Or: \[\begin{aligned} V(X)&= E\left[X^2-2XE(X)+E^2(X)\right] \\ &=E(X^2)-E[2XE(X)]+ E[E^2(X)]\\ &=E(X^2)-2E^2(X)+E^2(X) \\ &=E(X^2)-E^2(X) \end{aligned}\]

On cherche \(V(X)\) où \(X\) est le nombre obtenu lors du jet d’un dé équilibré. On a vu dans l’exemple que \(E(X) = \frac{7}{2}\). De plus,

\[\begin{aligned} E(X^2) &= 1^2 \bigg(\frac{1}{6}\bigg) + 2^2 \bigg(\frac{1}{6}\bigg) + 3^2 \bigg(\frac{1}{6}\bigg) + 4^2 \bigg(\frac{1}{6}\bigg) + 5^2 \bigg(\frac{1}{6}\bigg) + 6^2 \bigg(\frac{1}{6}\bigg) \\ &=\bigg(\frac{1}{6}\bigg) (91) = \frac{91}{6}.\end{aligned}\] Et donc

\[V(X) = \frac{91}{6} - \bigg(\frac{7}{2}\bigg)^2 = \frac{35}{12}\]

Propriétés de la variance

1. \(V(X) \geq 0\)

2. \(V(X+a)=V(X)\)
   en effet: \[\begin{aligned} V(X+a) &= E\big[\left[X+a-E(X+a)\right]^2\big] \\ &=E\big[\left[X+a-E(X)-a\right]^2\big] \\ &=E\big[\left[X-E(X)\right]^2\big] \\ &=V(X). \end{aligned}\]

3. \(V(aX)=a^2V(X)\)
   en effet: \[\begin{aligned} V(aX) &= E\big[\left[aX-E(aX)\right]^2\big] \\ &=E\big[\left[aX-aE(X)\right]^2\big] \\ &=E\big[a^2\left[X-E(X)\right]^2\big] \\ &=a^2\big[E\left[X-E(X)\right]^2\big] \\ &= a^2V(X). \end{aligned}\]

Ecart-type

Définition 1.5 La racine carrée de \(V(X)\) est appelée l’écart-type de \(X\), qui se note \(\sigma_{X}\). On a

\[\sigma_{X} = \sqrt{V(X)}\]

\(\sigma_{X}\) s’exprime dans les mêmes unités de mesure que la variable aléatoire \(X\).

A noter:

• L’écart type sert à mesurer la dispersion d’un ensemble de données.

• Plus il est faible, plus les valeurs sont regroupées autour de la moyenne.

• Exemple: La répartition des notes d’une classe. Plus l’écart type est faible, plus la classe est homogène.

• L’espérance et l’écart-type sont reliés par l’inégalité de Bienaymé-Tchebychev.

Inégalité de Bienaymé-Tchebychev

Théorème 1.2 Soit \(X\) une variable aléatoire d’espérance \(\mu\) et de variance \(\sigma^2\). Pour tout \(\varepsilon > 0\), on a l’inégalité suivante: \[P\left(|X-E(X)| \geq \varepsilon \right) \leq \frac{\sigma^2}{\varepsilon^2}\]

On peut l’écrire autrement. Soit \(k=\varepsilon/\sigma\). \[P\left(|X-E(X)| \geq k\sigma \right) \leq \frac{1}{k^2}\]

Importance: Cette inégalité relie la probabilité pour \(X\) de s’écarter de sa moyenne \(E(X)\), à sa variance qui est justement un indicateur de dispersion autour de la moyenne de la loi. Elle montre quantitativement que “plus l’écart type est faible, plus la probabilité de s’écarter de la moyenne est faible”.

Théorème 1.3 (Inégalité de Markov) Soit \(X\) une variable aléatoire à valeur non négatives. Pour tout réel \(a > 0\) \[P(X>a) \leq \frac{E(X)}{a}\]

Moments non centrés et centrés

On appelle moment non centré d’ordre \(r \in \mathbb{N^*}\) de \(X\) la quantité, lorsqu’elle existe: \[m_{r}(X)=\sum_{i \in \mathbb{N} } x_{i}^r p(x_{i})=E(X^r).\] Le moment centré d’ordre \(r \in \mathbb{N^*}\) est la quantité, lorsqu’elle existe: \[\mu_{r}(X)=\sum_{i \in \mathbb{N} } p_{i}\left[x_{i}-E(X)\right]^r=E\left[X-E(X)\right]^r.\]

Les premiers moments sont: \[m_{1}(X)=E(X), \quad \mu_{1}(X)=0\] \[\mu_{2}(X)=V(X)=m_{2}(X)-m_{1}^2(X)\]