Chapitre 2 Échantillonnage et Théorèmes limites

2.1 Échantillonnage

L’étude d’une caractéristique d’une pièce fabriquée en grand nombre (telle que la luminosité d’une ampoule, sa durée de vie ou encore le diamètre d’une pièce mécanique) relève, elle aussi, de la statistique descriptive. Il n’est toutefois pas possible de mesurer cette caractéristique sur toutes les pièces produites. Il est alors nécessaire de se limiter à l’étude des éléments d’un échantillon. Cet échantillon devra répondre à des critères particuliers pour pouvoir représenter la population toute entière dans l’étude statistique.

La démarche statistique présente plusieurs étapes :

• Prélèvement d’un échantillon représentatif de la population ou échantillon aléatoire par des techniques appropriées. Cela relève de la théorie de l’échantillonnage.
• Étude des caractéristiques de cet échantillon, issu d’une population dont on connaît la loi de probabilité. On s’intéresse principalement à ceux issus d’une population gaussienne.

Définition 2.1 \iffalse (Echantillon) Un échantillon aléatoire est un \(n\)-uplet \((X_1,\ldots,X_n)\) de \(n\) variables aléatoires indépendantes suivant la même loi qu’une variable \(X\) appelée variable aléatoire parente. Une réalisation de l’échantillon sera notée \((x_1,\ldots,x_n)\).

Définition 2.2 \iffalse (Une statistique) Soit \(X\) une variable aléatoire. Considérons un \(n\)-échantillon \((X_1,\ldots,X_n)\) de \(X\). Une Statistique \(T\) est une variable aléatoire fonction mesurable de \((X_1,\ldots,X_n)\).

\[ T(X)=T(X_1,\ldots,X_n) \]

A un échantillon, on peut associer plusieurs statistiques.

2.2 La statistique \(\overline{X}_n\)

Définition 2.3 \iffalse (Moyenne empirique) La statistique \(\overline{X}_n\) ou moyenne empirique d’un échantillon est une statistique définie par \[\overline{X}_n = \frac{1}{n} \sum_{i=1}^n X_i\]

Espérance et variance de \(\overline{X}_n\):

Soit \(m\) l’espérance et \(\sigma^2\) la variance de la variable parente \(X\) (e.g. l’espérance et la variance de la population). L’espérance et la variance de la statistique \(\overline{X}_n\) sont:

\[E(\overline{X}_n) = m\] \[V(\overline{X}_n) = \frac{\sigma^2}{n}\]

Démonstration:

• \(E(\overline{X}_n) = \frac{1}{n} \sum_{i=1}^n E(X_i) = \frac{1}{n} nm = m\)
• \(V(\overline{X}_n) =V(\frac{1}{n} \sum_{i=1}^n X_i) = \frac{1}{n^2} V(\sum_{i=1}^n X_i) = \frac{1}{n^2} \sum_{i=1}^n V(X_i) = \frac{1}{n^2} \sum_{i=1}^n \sigma^2 = \frac{1}{n^2} n \sigma^2 = \frac{\sigma^2}{n} \quad \quad\) (Les \(X_i\) étant supposées indépendantes)

2.3 Théorèmes limites

Cette section introduit trois résultats importants de la théorie asymptotique des probabilités: la loi faible des grands nombres, la loi forte des grands nombres et le théorème central limite, dans sa version pour variables aléatoires indépendantes et identiquement distribuées (\(X_i\) suivent la même loi pour \(i=1,\ldots,n\)). Ce sont des résultats qui traitent les propriétés de la distribution de la statistique \(\overline{X}_n\).

Des variables aléatoires indépendantes et identiquement distribuées (i.i.d) sont des variables aléatoires indépendantes qui suivent la même loi de probabilité, donc ont la même espérance et la même variance.

Les deux lois des grands nombres énoncent les conditions sous lesquelles la moyenne d’une suite de variables aléatoires converge vers leur espérance commune et expriment l’idée que lorsque le nombre d’observations augmente, la différence entre la valeur attendue (\(m = E(X)\)) et la valeur observée (\(\overline{X}_n\)) tend vers zéro. De son côté, le théorème central limite établit que la distribution standardisée d’une moyenne tend asymptotiquement vers une loi normale, et cela même si la distribution des variables sous-jacentes est non normale. Ce résultat est central en probabilités et statistique et peut être facilement illustré (cf. figure 2.1). Indépendamment de la distribution sous-jacente des observations (ici une loi uniforme), lorsque \(n\) croît, la distribution de \(\overline{X}_n\) tend vers une loi normale: on observe dans l’illustration la forme de plus en plus symétrique de la distribution ainsi que la concentration autour de l’espérance (ici \(m = 0.5\)) et la réduction de la variance.

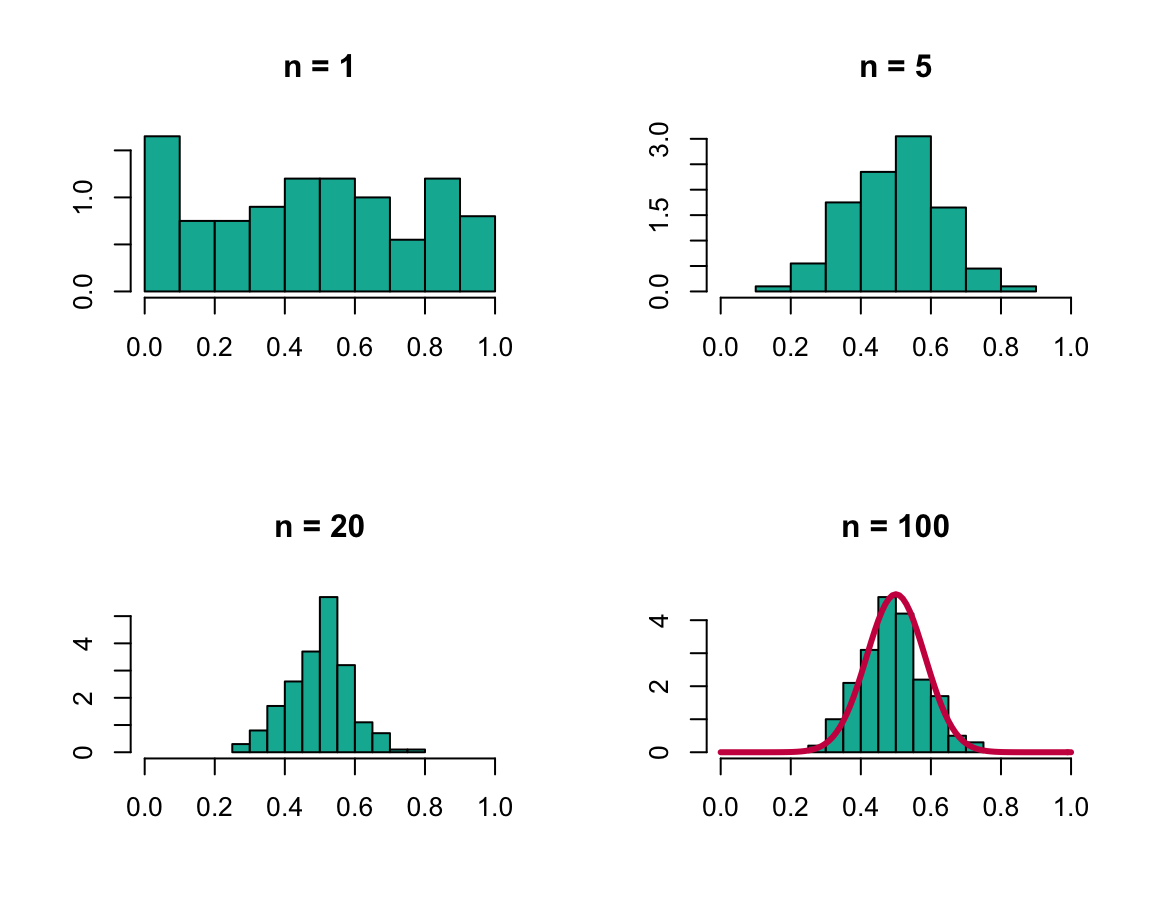
Figure 2.1: Illustration du théorème central limite: histogramme de la moyenne de 200 échantillons issus d’une loi uniforme sur l’intervalle (0,1) en fonction de la taille \(n\) de l’échantillon.

Les retombées pratiques de ces résultats sont importantes. En effet, la moyenne de variables aléatoires est une quantité qui intervient dans plusieurs procédures statistiques. Aussi, le résultat du théorème central limite permet l’approximation des probabilités liées à des sommes de variables aléatoires (e.g. méthode de Monte-Carlo). De plus, lorsque l’on considère des modèles statistiques, le terme d’erreur représente la somme de beaucoup d’erreurs (erreurs de mesure, variables non considérées, etc.). En prenant comme justification le théorème central limite, ce terme d’erreur est souvent supposé se comporter comme une loi normale.

2.3.1 Loi faible des grands nombres

Théorème 2.1 \iffalse (Loi faible des grands nombres) Soit \(X_1,\ldots,X_n\) une suite de variables aléatoires indépendantes et identiquement distribuées. On suppose que \(E(|X_i|) < \infty\) et que tous les \(X_i\) admettent la même espérance \(E(X_i)=m\). Alors:

\[\overline{X}_n = \frac{1}{n} \sum_{i=1}^n X_i \rightarrow m \quad \text{au sens de la convergence en probabilités}\]

càd \(\forall \varepsilon > 0, \lim_{n \to \infty} P(|\overline{X}_n - m|> \varepsilon) = 0\).

\(\overline{X}_n \text{ converge en probabilité vers } m \text{ quand } n \rightarrow +\infty\).

2.3.2 Loi forte des grands nombres

Théorème 2.2 \iffalse (Loi forte des grands nombres) Soit \(X_1,\ldots,X_n\) une suite de variables aléatoires indépendantes et identiquement distribuées. On suppose que \(E(|X_i|) < \infty\) et que tous les \(X_i\) admettent la même espérance \(E(X_i)=m\). Alors:

\[\overline{X}_n = \frac{1}{n} \sum_{i=1}^n X_i \rightarrow m \quad \text{presque sûrement}\]

càd \(P\big( \lim_{n \to \infty} \overline{X}_n = m\big) = 1\).

\(\overline{X}_n \text{ converge presque sûrement vers } m\)

Illustration de la loi des grands nombres

Prenons l’exemple d’un lancer de dé équilibré. On lance un dé et on note \(X\) le résultat obtenu. La loi de \(X\) est la suivante:

\(x_i\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
\(P(X = x_i)\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)

Et donc l’espérance de \(X\) est \(E(X)=\sum_i p_i x_i = 3.5\). Pour illustrer le théorème on va procéder à un échantillonnage. On répète le lancement du dé \(n\) fois. A chaque \(n\) on va calculer la moyenne empirique des résultats obtenus, qu’on va noter \(\overline{X}_n\). Selon la loi de grands nombre cette moyenne va converger vers l’espérance théorique:

\[\overline{X}_n \rightarrow E(X)=m=3.5 \quad \text{quand} \quad n \rightarrow \infty\]

Traçons l’évolution de la moyenne empirique en fonction de la taille \(n\) de l’échantillon, dans deux différents échantillonnages aléatoires:

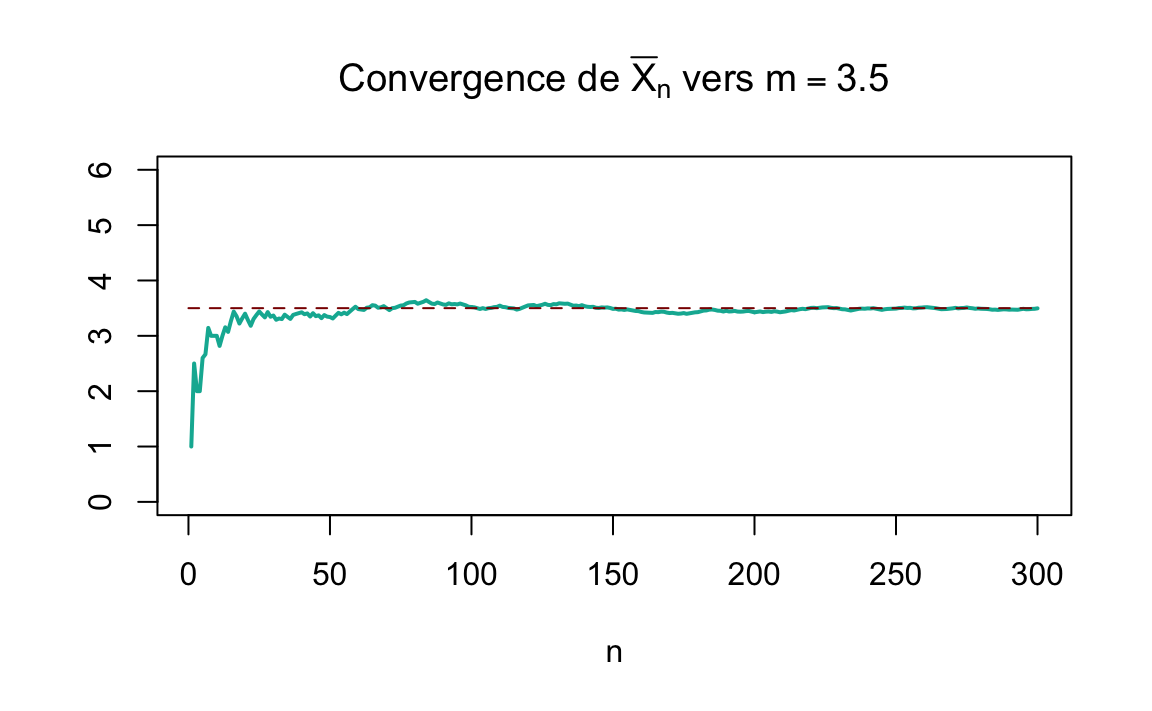
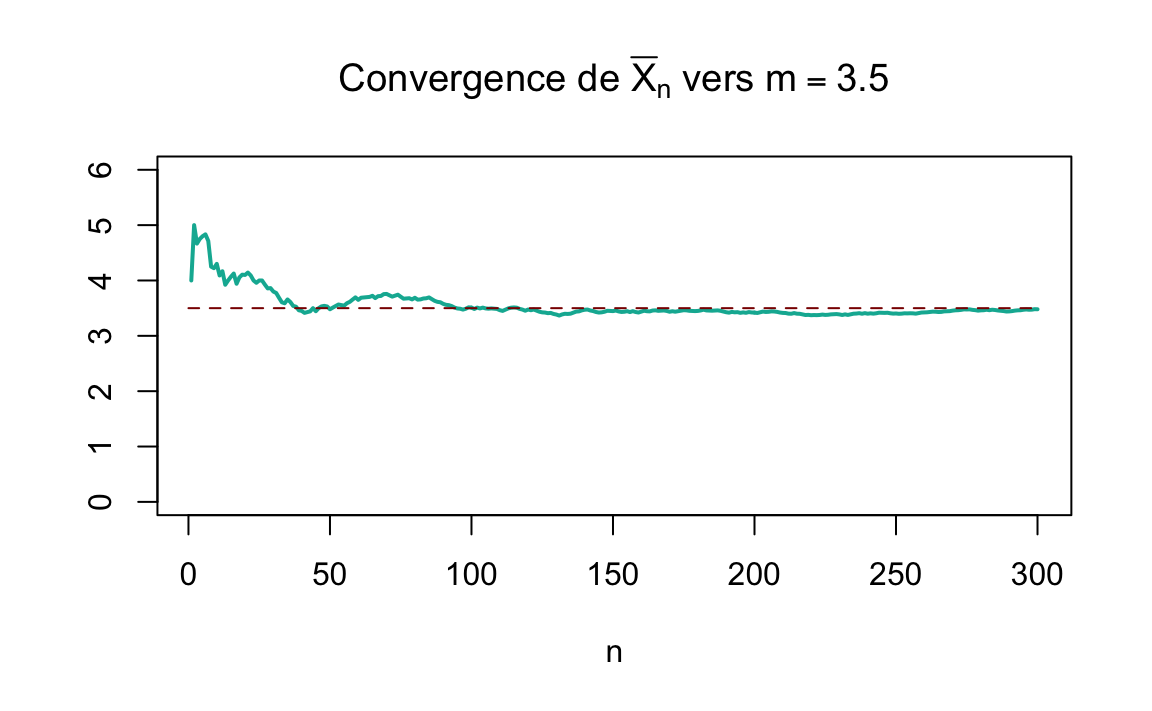
Figure 2.2: Convergence de \(\overline{X}_n\) vers \(m=3.5\) pour deux différents échantillonnages

2.3.3 Théorème central limite

Théorème 2.3 \iffalse (Théorème central limite) Soit \(X_1,\ldots,X_n\) une suite de variables aléatoires indépendantes et identiquement distribuées, d’espérance \(m\) et variance \(\sigma^2\) finie. Alors

\[\begin{equation} \frac{\overline{X}_n - m}{ \sigma/\sqrt{n}} \xrightarrow{n \to \infty} \mathcal{N}(0,1) \quad \text{en distribution} \tag{2.1} \end{equation}\]

On voit bien que, afin que la convergence se fasse, une standardisation est nécessaire: en effet, on peut voir le rapport dans (2.1) comme

\[\frac{\overline{X}_n - m}{ \sigma/\sqrt{n}} = \frac{\overline{X}_n - E(\overline{X}_n)}{ \sqrt{var(\overline{X}_n)}}\]

Notes Historiques

La loi faible des grands nombres a été établie la première fois par J. Bernoulli pour le cas particulier d’une variable aléatoire binaire ne prenant que les valeurs 0 ou 1. Le résultat a été publié en 1713.

La loi forte des grands nombres est due au mathématicien E. Borel (1871- 1956), d’où parfois son autre appellation: théorème de Borel.

Le théorème central limite a été formulé pour la première fois par A. de Moivre en 1733 pour approximer le nombre de “piles” dans le jet d’une pièce de monnaie équilibrée. Ce travail a été un peu oublié jusqu’à ce que P.S. Laplace ne l’étende à l’approximation d’une loi binomiale par la loi normale dans son ouvrage Théorie analytique des probabilités en 1812. C’est dans les premières années du \(XX^e\) siècle que A. Lyapounov l’a redéfini en termes généraux et prouvé avec rigueur.

Application 1:

Pour une taille d’échantillon \(n\) suffisamment grande, on peut considérer que \(\overline{X}_n\) a pour loi:

\[ \overline{X}_n \thicksim \mathcal{N}\big(m, \frac{\sigma^2}{n}\big)\]

Dans la notation de la loi normale ci dessus \(\frac{\sigma^2}{n}\) est la variance. \(\frac{\sigma}{\sqrt{n}}\) est l’écart-type.

Application 2: la loi d’un pourcentage, étudiée dans la section suivante.

2.4 Loi d’un pourcentage

Soit \(X\) la variable aléatoire représentant le nombre de succès au cours d’une suite de \(n\) répétitions indépendantes d’une même épreuve dont la probabilité de succès est \(p\).

La loi de \(X\) est la loi binomiale de paramètres \(n\) et \(p\) notée \(\mathcal{B}(n, p)\). \(X\) est la somme de \(n\) variables indépendantes de Bernoulli de paramètre \(p\).

Notons \(P_n\) la fréquence empirique du nombre de succès parmi les \(n\) épreuves:

\[P_n= \frac{X}{n}\]

\(P_n = \overline{X}_n\) car \(X\) est la somme de \(n\) variables indépendantes de Bernoulli de paramètre \(p\).

\(P_n\) a pour espérance et pour variance:

\[E(P_n) = p \quad \quad \text{et} \quad \quad V(P_n) = \frac{p(1-p)}{n}\]

En appliquant le théorème central limite à \(X\) somme des variables de Bernoulli:

\[ \text{Pour } n \text{ suffisamment grand, on peut considérer que } P_n \text{ suit la loi normale :}\] \[P_n \thicksim \mathcal{N}\bigg(p, {\frac{p(1-p)}{n}}\bigg)\]

Ce résultat est une autre formulation du théorème de “De Moivre-Laplace” (lien).

2.5 Etude de la statistique \(S^2\)

Définition 2.4 \iffalse (Variance empirique) La statistique \(S_n^2\) ou variance empirique d’échantillon est définie par: \[S_n^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\overline{X}_n\right)^{2}\]

Propriétés:

• \(S_n^{2}=\frac{1}{n} \big(\sum_{i=1}^{n}X_{i}^2\big)-\big(\overline{X}_n\big)^{2}\).
• \(S_n^{2}=\frac{1}{n} \sum_{i=1}^{n}\big(X_{i}-m\big)^2-\big(\overline{X}_n-m\big)^{2}\).
• \(S_n^{2} \text{ converge presque sûrement vers } \sigma^2\).

Espérance de \(S_n^{2}\):

• L’espérance de \(S_n^{2}\) est:

\[E(S_n^{2}) = \frac{n-1}{n}\sigma^2\]

démonstration:

\[\begin{align} E(S_n^{2}) & =\frac{1}{n} \sum_{i=1}^{n}E\big(X_{i}-m\big)^2-E\big(\overline{X}_n-m\big)^{2} \\ & = \frac{1}{n} \sum_{i=1}^{n}V(X_i)-V(\overline{X}_n) \\ & = \frac{1}{n} \sum_{i=1}^{n}\sigma^2- \frac{\sigma^2}{n} = \sigma^2- \frac{\sigma^2}{n} = \frac{n-1}{n} \sigma^2 \end{align}\]

On peut remarquer que si on pose: \({S_n^{*}}^2 = \frac{n}{n-1}S_n^2\) alors \(E({S_n^{*}}^2) = \sigma^2\).

2.6 Introduction à l’estimation

On appelle estimation, la procédure d’utilisation des informations obtenues à partir d’un échantillon qui permet de déduire des résultats concernant l’ensemble de la population.

Dans ce cours, les estimations sont calculées à partir d’un échantillonnage aléatoire simple et avec remise, càd tous les individus de la population ont une probabilité égale de faire partie de l’échantillon et qu’un individu peut être choisi plus d’une fois.

La statistique inconnue d’une population, à estimer à partir d’un échantillon, est appelée un paramètre. Souvent le paramètre à estimer est une moyenne, un total, une proportion, un écart-type ou une variance. Le paramètre de la population est estimé à partir d’une estimation elle même calculée à partir des données d’un échantillon.

Le tableau ci dessous illustre les différents symboles souvent utilisés.

	Paramètres population	Estimations calculées sur un échantillon de taille \(n\)
Moyenne	\(m\)	\(\overline{X}_n=\hat{m}\)
Ecart-type	\(\sigma\)	\(S_n=\hat{\sigma}\)
Variance	\(\sigma^2\)	\(S_n^2=\hat{\sigma}^2\)
Proportion	\(p\)	\(P_n=\hat{p}\)

On dit que \(\overline{X}_n\) est un estimateur de \(m\). La valeur obtenue est une estimation de \(m\), qu’on appelle \(\hat{m}\).

Les estimateurs sont des variables aléatoires et les estimations sont les valeurs observées des estimateurs (i.e des variables aléatoires).

Dans ce chapitre nous avons introduit des estimateurs de la moyenne, la variance et la proportion. Nous avons aussi étudié les lois de ces estimateurs. Dans le chapitre suivant, nous allons étudier la théorie de l’estimation ponctuelle et la recherche d’un estimateur.