TP estimation
Il faut finir les TPs de la 1ère et 2ème séances avant de commencer ce TP.
3.8 Comparaison d’estimateurs
Soit \(\left(X_{1}, \ldots, X_{n}\right)\) un échantillon de la loi uniforme sur \([0, \theta]\) où \(\theta\) est un paramètre inconnu.
On considère les estimateurs convergents (on dit aussi consistants) suivants du paramètre \(\theta\).
\[ \begin{aligned} T_{1}=& \frac{2}{n} \times\left(X_{1}+\ldots+X_{n}\right) \\ T_{2}=& \sqrt{\frac{3}{n} \times\left(X_{1}^{2}+\ldots+X_{n}^{2}\right)} \\ T_{3}=&\left(\frac{4}{n} \times\left(X_{1}^{3}+\ldots+X_{n}^{3}\right)\right)^{\frac{1}{3}} \\ T_{4}=&\left(\frac{3}{2 n} \times(\sqrt{X_{1}}+\ldots+\sqrt{X_{n}})\right)^{2} \\ T_{5}=&\left(\frac{1}{2 n} \times\left(\frac{1}{\sqrt{X_{1}}}+\ldots+\frac{1}{\sqrt{X_{n}}}\right)\right)^{-2} \\ T_{6}=& \exp (1) \times\left(X_{1} \times \ldots \times X_{n}\right)^{\frac{1}{n}} \\ T_{7}=& \max \left\{X_{1}, \ldots, X_{n}\right\} \\ T_{8}=& \frac{n+1}{n} \max \left\{X_{1}, \ldots, X_{n}\right\} \end{aligned} \]
- \(T1\) est l’emm de \(\theta\).
- \(T7\) est l’emv de \(\theta\) (biaisé).
- \(T8\) est l’emv corrigé de \(\theta\).
1. Choisir une valeur de \(\theta\) et simuler 1000 échantillons de taille 100 de la loi uniforme sur \([0, \theta]\). Calculer pour chacun de ces échantillons la valeur prise par les 8 estimateurs.
On pourra ensuite créer une matrice ayant 1000 lignes et 8 colonnes dont la jème colonne contient les 1000 réalisations de l’estimateur \(T_{j}\):
T <- cbind(T1,T2,T3,T4,T5,T6,T7,T8)2. Calculer la moyenne empirique et la variance empirique des 8 échantillons de taille 1000 ainsi obtenus. En déduire une estimation du biais et de l’erreur quadratique de chacun des 8 estimateurs.
On rappelle que pour un estimateur \(T\), le biais est \(E[T]-\theta\) et l’erreur quadratique est \(E\left[(T-\theta)^{2}\right]\).
3. Quels estimateus sont les moins biaisés? Et les estimateurs de risque quadratique minimale?
4. Représenter sur un même graphique les boites à moustaches (boxplots) des 8 estimateurs. Superposer sur le même graphique la vraie valeur du paramètre, en rouge. Commenter la pertinence de chacun des estimateurs: lequel préfereriez-vous utiliser?
On pourra utiliser
boxplot(data.frame(T))
abline(h=theta,col="red")3.9 Le maximum de vraisemblance
Pour cette partie, imaginons qu’on a une série de valeurs, ça peut par exemple être l’âge de 1000 étudiants pris au hasard dans une ville. Nous avons tracé l’histogramme de l’échantillon et obtenu le suivant:
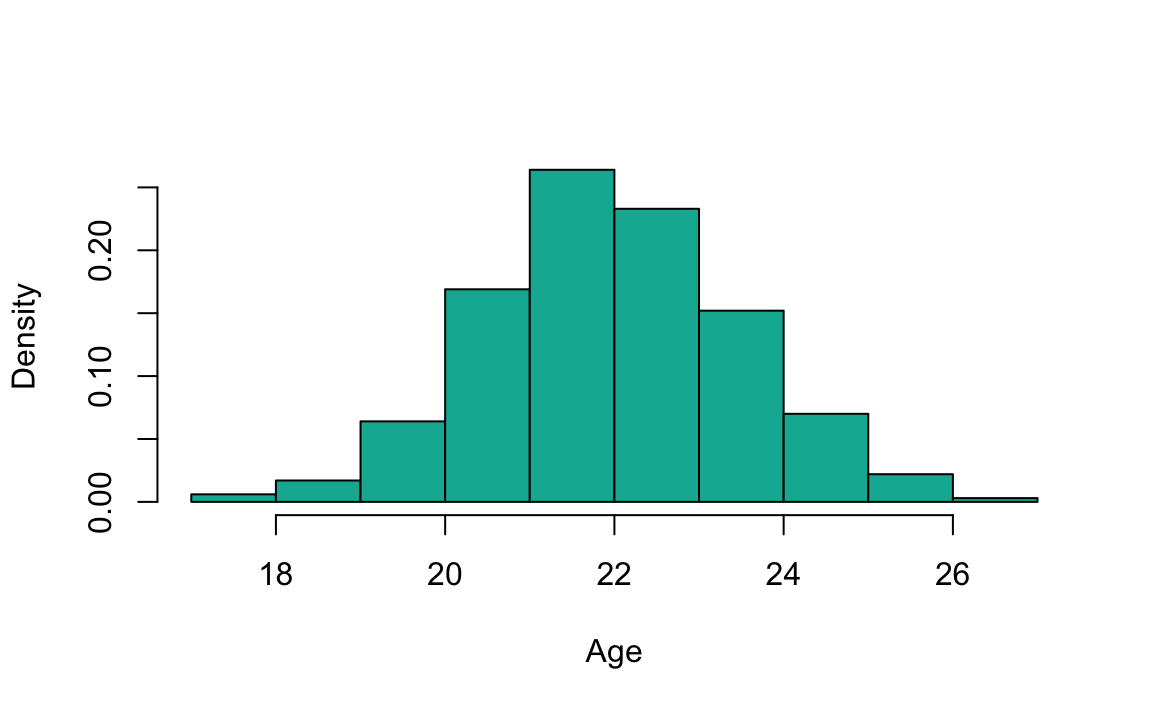
On peut voir ici que la distribution des valeurs suit approximativement une loi normale avec une moyenne aux alentours de 22 et un écart-type difficile à évaluer au premier coup d’oeil.
En effet, pour obtenir les données de cet échantillon, j’ai généré un échantillon suivant la loi normale de moyenne 22 et d’écart-type mystère que vous devez découvrir en utilisant la méthode du maximum de vraisemblance. Les données ont été générée avec la commande suivante:
data = rnorm(1000, mean = 22, sd = mystere) # où j'ai caché ici la valeur mystère de l'écart-type utilisé.Les données de l’échantillon obtenu se trouvent dans le fichier mystere.txt.
Pour lire les données de l’échantillon du fichier mystere.txt, vous pouvez les copier et les saisir dans un vecteur en utilisant la fonction c() ou bien utiliser la fonction scan().
Par exemple: donnees <- scan("mystere.txt", sep=",")
Sur l’intervalle \([1,4]\), chercher la valeur de \(\sigma\) qui maximise la vraisemblance. On la notera \(\hat{\sigma}\). On procédera de façon empirique en représentant le graphe de la Log-vraisemblance sur l’intervalle \([1,4]\). On se contentera d’une valeur approchée de \(\hat{\sigma}\) à \(10^{−1}\) près. Quelle estimation de \(\sigma\) par maximum de vraisemblance proposez-vous?
Re-tracer ensuite l’histogramme montré ci dessus en superposant la densité de la loi normale de moyenne 22 et d’écart-type estimé.
3.10 Loi de Weibull
En fiabilité, la durée de vie \(X\) d’un composant électronique est souvent modélisée par une loi de Weibull de paramètre \(\theta>0\). Une variable aleatoire \(X\) distribuée selon une loi de Weibull de paramètre \(\theta\) a pour densité:
\[\begin{equation} f(x)=\theta x^{\theta-1} \exp (-x^{\theta}) \, \times \, 1_{\mathbb{R}^+} \tag{3.1} \end{equation}\]
A noter que quand \(\theta=1\) la loi de Weibull coincide avec la loi Exponentielle de paramètre égal à \(1\).
L’interprétation du paramètre \(\theta\) est la suivante. Quand \(\theta>1\) cela signifie que la propension à tomber en panne à l’instant \(t\) augmente avec \(t\), quand \(\theta<1\), c’est l’inverse. Enfin, quand \(\theta=1\) la propension à tomber en panne à l’instant \(t\) ne dépent pas de \(t\) (la loi exponentielle est sans mémoire). On entend ici par panne toute défaillance du composant électronique rendant celui-ci hors d’usage.
1. Représenter le graphe de la densité d’une loi de Weibull quand \(\theta = 1/2, 1, 2,\text{et } 3\). On se limitera à l’intervalle \([0,5]\) pour \(x\). Pour cette question, vous devez créer la fonction dweibull qui calcule la densité comme définie dans l’équation (3.1).
Pour estimer \(\theta\) on dispose de la durée de vie de \(n=1000\) composants. Les données (en milliers d’heures) se trouvent dans le fichier weibull.txt.
2. Chercher la valeur de \(\theta\) qui maximise la vraisemblance. (\(\theta \in [0,5]\)). On la notera \(\hat{\theta}\).
3. Afficher l’histogramme de l’échantillon et superposer la densité de Weibull de paramètre \(\hat{\theta}\).