Chapitre 5 Tests d’hypothèses

5.1 Introduction: le problème de décision

Dans tous les domaines, de l’expérimentation scientifique à la vie quotidienne, on est amené à prendre des décisions sur une activité risquée au vu de résultats d’expériences ou d’observation de phénomènes dans un contexte incertain. Par exemple:

Informatique: au vu des résultats des tests d’un nouveau système informatique, on doit décider si ce système est suffisamment fiable et performant pour être mis en vente.
Essais thérapeutiques: décider si un nouveau traitement médical est meilleur qu’un ancien au vu du résultat de son expérimentation sur des malades.
Finance: au vu du marché, décider si on doit ou pas se lancer dans une opération financière donnée.

Dans chaque cas, le problème de décision consiste à trancher, au vu d’observations, entre une hypothèse appelée hypothèse nulle, notée $H_0$, et une autre hypothèse dite hypothèse alternative, notée $H_1$. En général, on suppose qu’une et une seule de ces deux hypothèses est vraie. Un test d’hypothèses est une procédure qui permet de choisir entre ces deux hypothèses.

Dans un problème de décision, deux types d’erreurs sont possibles:

Erreur de première espèce: décider que $H_1$ est vraie alors que $H_0$ est vraie.
Erreur de seconde espèce: décider que $H_0$ est vraie alors que $H_1$ est vraie.

Les conséquences de ces deux erreurs peuvent être d’importances diverses. En général, une des erreurs est plus grave que l’autre:

Informatique: si on conclut à tort que le système n’est pas assez fiable et performant, on engagera des dépenses inutiles pour le tester et l’analyser et on risque de se faire souffler le marché par la concurrence; si on décide à tort qu’il est suffisamment fiable et performant, on va mettre en vente un produit qui ne satisfera pas la clientèle, ce qui peut coûter cher en image de marque comme en coût de maintenance.
Essais thérapeutiques: on peut adopter un nouveau traitement moins efficace, voire pire que l’ancien, ou se priver d’un nouveau traitement plus efficace que l’ancien.
Finance: si on décide à tort que l’on peut lancer l’opération, on risque de perdre beaucoup d’argent; si on décide à tort de ne pas lancer l’opération, on peut se priver d’un bénéfice important.

A toute décision correspond une probabilité de décider juste et une probabilité de se tromper:

La probabilité de l’erreur de première espèce, qui est la probabilité de rejeter à tort $H_0$, est notée $\alpha$ et est appelée seuil ou niveau de signification du test. C’est la même terminologie que pour les intervalles de confiance, ce qui n’est pas un hasard¹⁰. Dans certains contextes, cette probabilité est appelée risque fournisseur.
La probabilité de l’erreur de deuxième espèce est notée $\beta$ et est parfois appelée risque client. C’est la probabilité d’accepter à tort $H_0$.
La probabilité de décider $H_1$ ou de rejeter $H_0$ à raison est $1-\beta$. Elle est appelée puissance du test.
$1-\alpha$ est appelée niveau de confiance du test.

Les deux tableaux suivants résument simplement le rôle de ces probabilités.

Décision $\backslash$ Vérité	$H_0$	$H_1$
$H_0$	conclusion correcte	erreur de deuxième espèce
$H_1$	erreur de première espèce	conclusion correcte

Décision $\backslash$ Vérité	$H_0$	$H_1$
$H_0$	niveau de confiance $1-\alpha$	risque $\beta$
$H_1$	risque $\alpha$	Puissance de test $1-\beta$

L’idéal serait évidemment de trouver une procédure qui minimise les deux risques d’erreur en même temps. Malheureusement, on montre qu’ils varient en sens inverse, c’est- à-dire que toute procédure diminuant $\alpha$ va en général augmenter $\beta$ et réciproquement.

Dans la pratique, on va donc considérer que l’une des deux erreurs est plus importante que l’autre, et tâcher d’éviter que cette erreur se produise. Il est alors possible que l’autre erreur survienne. Par exemple, dans le cas du procès, on fait en général tout pour éviter de condamner un innocent, quitte à prendre le risque d’acquitter un coupable. On va choisir $H_0$ et $H_1$ de sorte que l’erreur que l’on cherche à éviter soit l’erreur de première espèce, $\alpha$.

Mathématiquement cela revient à se fixer la valeur du seuil du test $\alpha$. Plus la conséquence de l’erreur est grave, plus $\alpha$ sera choisi petit. Les valeurs usuelles de $\alpha$ sont $10\%$, $5\%$, $1\%$, ou beaucoup moins. Le principe de précaution consiste à limiter au maximum la probabilité de se tromper, donc à prendre $\alpha$ très petit.

On choisit $H_0$ et $H_1$ de sorte que l’erreur que l’on cherche à éviter soit l’erreur de première espèce, $\alpha$.
Le choix d’un test sera le résultat d’un compromis entre risque de premier espèce et puissance du test.

On appelle règle de décision une règle qui permette de choisir entre $H_0$ et $H_1$ au vu des observations $x_1 ,\ldots,x_n$, sous la contrainte que la probabilité de rejeter à tort $H_0$ est égale à $\alpha$ fixé. Une idée naturelle est de conclure que $H_0$ est fausse s’il est très peu probable d’observer $x_1 ,\ldots,x_n$ quand $H_0$ est vraie.

Par exemple, admettons que l’on doive décider si une pièce est truquée ou pas au vu de 100 lancers de cette pièce. Si on observe 90 piles, il est logique de conclure que la pièce est truquée et on pense avoir une faible probabilité de se tromper en concluant cela. Mais si on observe 65 piles, que conclure?

Une fois que l’on a fixé raisonnablement $\alpha$, il faut choisir une variable de décision, qui doit apporter le maximum d’information sur le problème posé, et dont la loi sera différente selon que $H_0$ ou $H_1$ est vraie. La loi sous $H_0$ doit être connue. On définit alors la région critique qui est l’ensemble des valeurs de la variable de décision qui conduisent à rejeter $H_0$ au profit de $H_1$. Sa forme est déterminée par la nature de $H_1$, et sa détermination exacte est donnée par $P(RC|H_0) = \alpha$. La région d’acceptation est son complémentaire $\overline{RC}$.

Remarque: il vaut mieux dire “ne pas rejeter $H_0$” que “accepter $H_0$”. En effet, si on rejette $H_0$, c’est que les observations sont telles qu’il est très improbable que $H_0$ soit vraie. Si on ne rejette pas $H_0$, c’est qu’on ne dispose pas de critères suffisants pour pouvoir dire que $H_0$ est fausse. Mais cela ne veut pas dire que $H_0$ est vraie.

Un test permet de dire qu’une hypothèse est très probablement fausse ou seulement peut-être vraie.

Par conséquent, dans un problème de test, il faut choisir les hypothèses $H_0$ et $H_1$ de façon à ce que ce qui soit vraiment intéressant, c’est de rejeter $H_0$.

5.1.1 Les tests unilatéraux et bilatéraux

Une hypothèse alternative bilatérale est appropriée lorsqu’on souhaite vérifier si le paramètre $\theta$ d’une distribution diffère d’une valeur arbitraire $\theta_0$. Par exemple, s’il est important de détecter les valeurs de la moyenne réelle $\mu$ plus grandes ou plus petites que $\mu_0$, on doit utiliser l’alternative bilatérale (seule $H_1$ est composite):

\[ H_{0}: \mu=\mu_{0} \text { contre } H_{1}: \mu\neq\mu_{0} \]

Par contre, supposons qu’on désire rejeter $H_0$ seulement lorsque la vraie valeur de la moyenne excède $\mu_0$. Ainsi, les hypothèses sont

\[ H_{0}: \mu \leq \mu_{0} \text { contre } H_{1}: \mu > \mu_{0} \]

La région critique est alors située dans l’aile supérieure de la distribution de la statistique. On rejette $H_0$ si $\overline{x}$ est trop grand. Ceci est un test unilatéral à droite ($H_0$ et $H_1$ sont composites).

Une troisième possibilité consiste à faire un test unilatéral à gauche en posant les hypothèses

\[ H_{0}: \mu \geq \mu_{0} \text { contre } H_{1}: \mu < \mu_{0} \]

On rejette alors $H_0$ lorsque la moyenne échantillonnale est trop petite.

Pour les règles de décision des tests unilatéraux, sous $H_0$ on suppose que $\mu=\mu_0$.
$H_0$ et $H_1$ sont complémentaires: une des deux hypothèses est forcément vraie.

5.1.2 Relation entre tests d’hypothèses bilatéraux et intervalles de confiance

Il existe une relation étroite entre le test d’une hypothèse sur un paramètre $\theta$ et l’intervalle de confiance pour $\theta$. Si $[L,U]$ est un intervalle de confiance de niveau $1-\alpha$ pour le paramètre $\theta$, alors le test de seuil $\alpha$ de l’hypothèse

\[ H_{0}: \theta=\theta_{0} \text { contre } H_{1}: \theta\neq \theta_{0} \]

mènera au rejet de $H_0$ si et seulement si $\theta_0$ n’appartient par à l’intervalle $[L,U]$.

Exemple 5.1 Considérons une situation où un intervalle de confiance de niveau $1-\alpha=0.95$ pour la moyenne d’une population a été calculé à partir d’un échantillon, et où on a obtenu $[41,43]$. Comme la valeur $40$ n’appartient pas à cet intervalle, alors on sait qu’en conduisant un test d’hypothèse sur le même échantillon, l’hypothèse $H_0 : \mu = 40$ sera rejetée au seuil $\alpha=0.05$, au profit de son alternative bilatérale.

5.1.3 La démarche générale d’un test d’hypothèse

Récapitulons l’ensemble de la démarche à suivre pour effectuer un test d’hypothèses:

Choisir $H_0$ et $H_1$ de sorte que ce qui importe, c’est le rejet de $H_0$.
Se fixer $\alpha$ selon la gravité des conséquences de l’erreur de première espèce.
Déterminer la région critique: établir la règle de rejet de $H_0$ à partir de la distribution de la statistique du test (lorsque $H_0$ est vraie).
Calculer la valeur observée de la statistique du test à partir de l’échantillon.
Comparer la valeur observée à la valeur critique: Regarder si les observations se trouvent ou pas dans la région critique.¹¹
Conclure au rejet ou au non-rejet de $H_0$.

5.1.4 Types de test d’hypothèses

On distingue différentes catégories de tests:

Les tests paramétriques ont pour objet de tester une certaine hypothèse relative à un ou plusieurs paramètres d’une variable aléatoire de loi spécifiée (généralement supposée normale). Lorsque le test est toujours valide pour des variables non gaussiennes, on dit que le test est robuste (à la loi).
Les tests non paramétriques qui portent généralement sur la fonction de répartition de la variable aléatoire, sa densité, etc.
Les tests libres (distributions free) qui ne supposent rien sur la loi de probabilité de la variable aléatoire étudiée (et qui sont donc robuste). Ces tests sont souvent non paramétriques, mais pas toujours.

On s’intéressera d’abord dans ce chapitre à des tests d’hypothèses paramétriques quand l’observation est un échantillon d’une loi de probabilité. Puis on étudiera dans les chapitres suivants des tests de comparaison de deux échantillons, et on terminera en présentant le plus célèbre des tests d’hypothèses, le test du $\chi^2$.

5.2 Les tests d’hypothèses à partir d’un seul échantillon

Dans cette section, nous abordons les détails de la procédure des tests d’hypothèses dans diverses situations: les tests sur la moyenne d’une distribution normale avec variance connue et inconnue, les tests sur la variance d’une distribution normale, et les tests sur une proportion (pour une grande taille d’échantillon).

5.2.1 Les tests sur la moyenne d’une distribution normale de variance connue

5.2.1.1 La procédure pour le test bilatéral

Supposons que la variable aléatoire $X$ représente un certain processus ou une certaine population d’intérêt. On suppose que $X$ suit une loi normale ou que, dans le cas contraire, le théorème central limite s’applique. De plus on suppose que la moyenne $\mu$ de $X$ est inconnue, mais que sa variance $\sigma^2$ est connue. On veut tester les hypothèses

\[ H_{0}: \mu=\mu_{0} \text { contre } H_{1}: \mu\neq\mu_{0} \]

où $\mu_0$ est une constante spécifiée.

Un échantillon aléatoire simple $X_1,\ldots,X_n$ de taille $n$ est disponible. Chaque observation dans cet échantillon a une moyenne théorique $\mu$ inconnue et une variance théorique $\sigma^2$ connue. Si l’hypothèse nulle $H_0: \mu = \mu_0$ est vraie, alors $\overline{X}_n \thicksim \mathcal{N}(\mu_0,\sigma^2/n)$. La procédure de test utilise la statistique:

\[ Z_0 = \frac{ \overline{X}_n - \mu_0 }{\sigma/\sqrt{n}} \] laquelle, sous l’hypothèse nulle, suit la loi normale centrée réduite $\mathcal{N}(0,1)$. Donc, si $H_0: \mu = \mu_0$ est vraie, la probabilité est $1-\alpha$ qu’une valeur de la statistique $Z_0$ soit entre $z_{\frac{\alpha}{2}}$ et $z_{1-\frac{\alpha}{2}}$, où $z_{1-\frac{\alpha}{2}}$ est le quantile de la loi normale centrée réduite tel que $P(Z_0 \geq z_{1-\frac{\alpha}{2}})=\alpha/2$. Les figures 5.1 et 5.2 illustrent respectivement la distribution de $\overline{X}_n$ et $Z_0$ lorsque $H_0$ est vraie.

#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'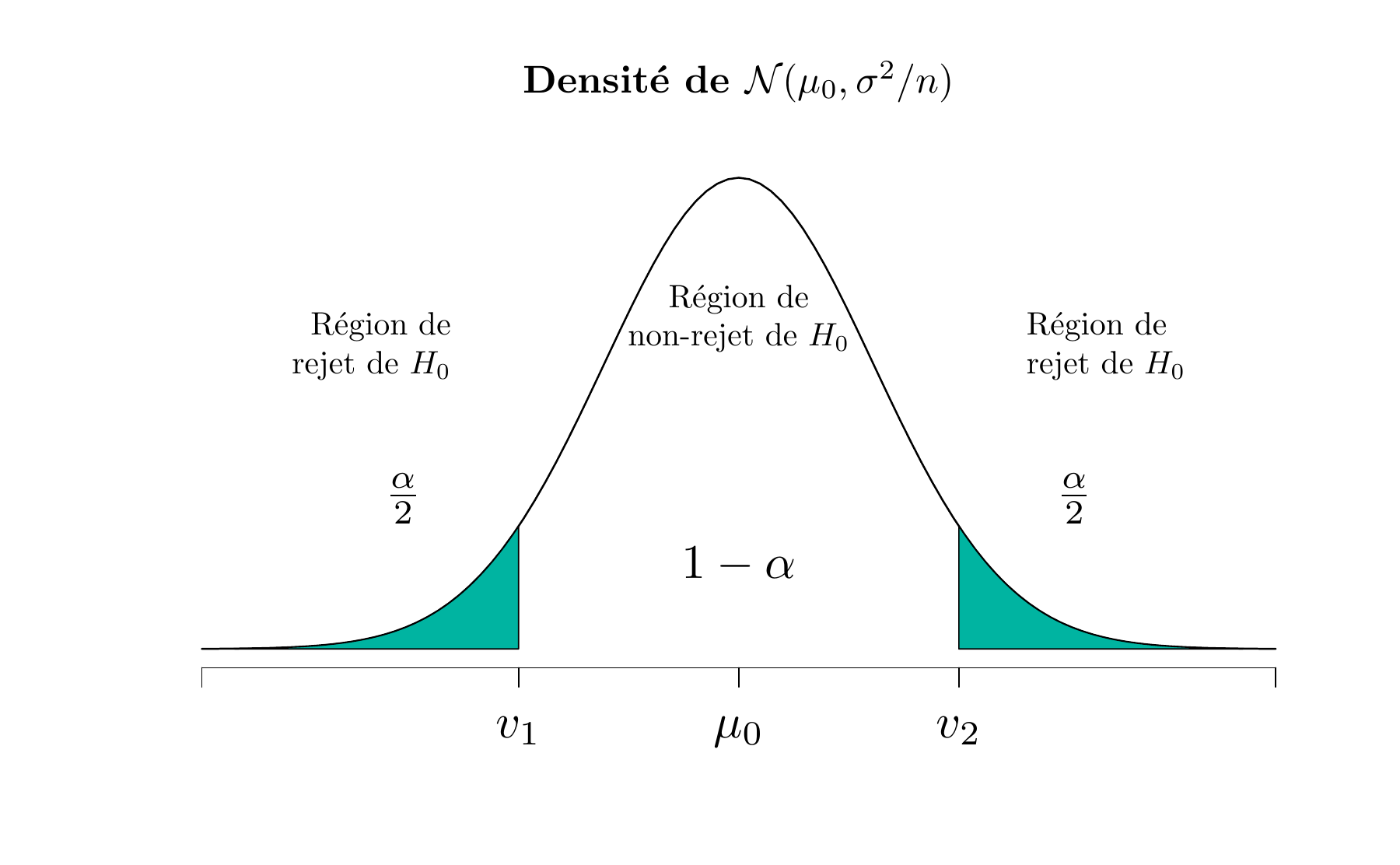

$La distribution de $\overline{X}_n$ lorsque $H_0 : \mu = \mu_0$ est vraie$

Figure 5.1: La distribution de $\overline{X}_n$ lorsque $H_0 : \mu = \mu_0$ est vraie

#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'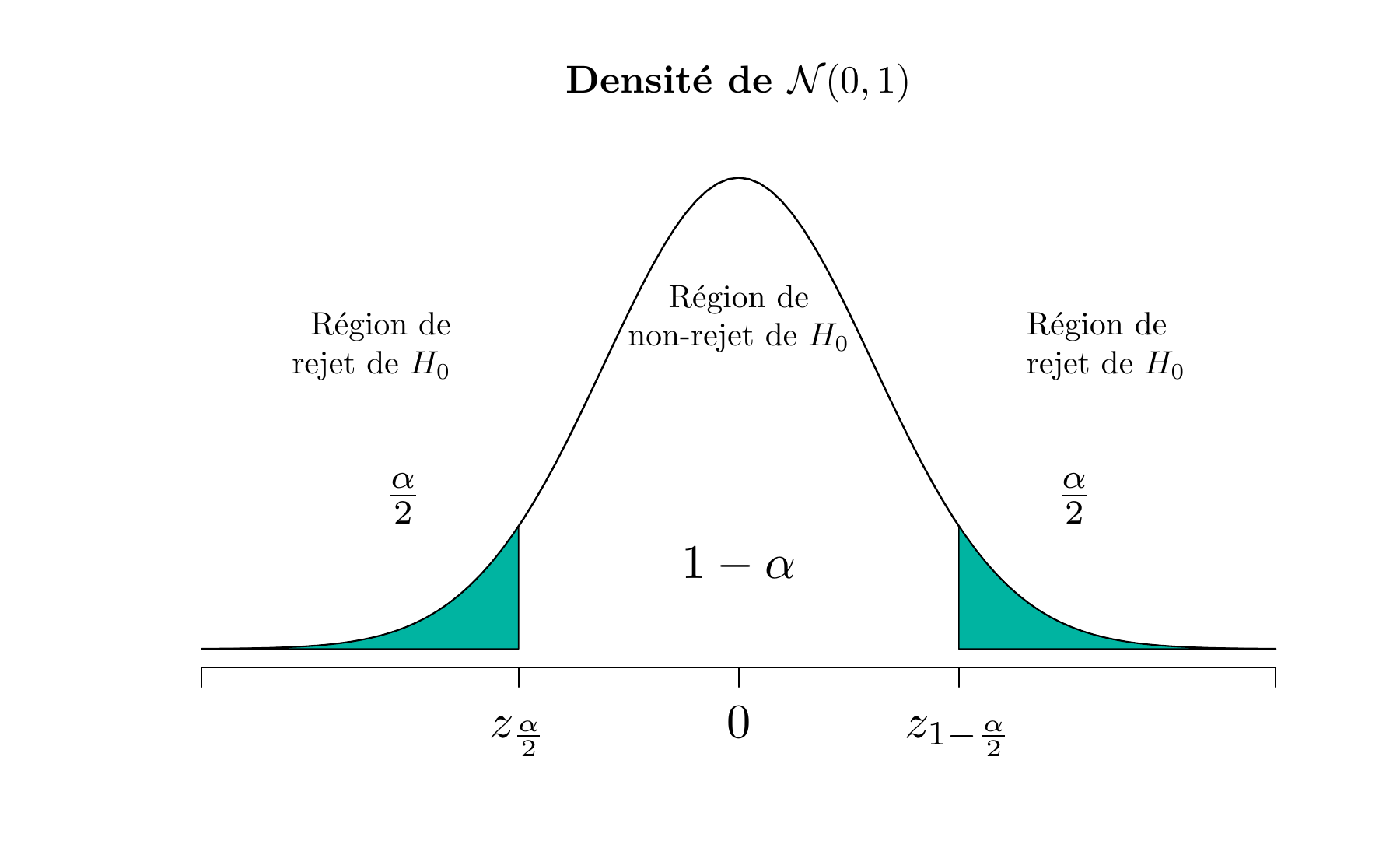

$La distribution de $Z_0$ lorsque $H_0 : \mu = \mu_0$ est vraie$

Figure 5.2: La distribution de $Z_0$ lorsque $H_0 : \mu = \mu_0$ est vraie

Visiblement, un échantillon donnant une valeur de la statistique qui appartient aux extrémités de la distribution de $Z_0$ est peu probable si $H_0: \mu = \mu_0$ est vraie. Le cas échéant, on aurait raison de remettre en doute la véracité de $H_0$.

Critère de rejet de $H_0: \mu = \mu_0$ (test bilatéral, loi normale, variance connue)

On se donne comme règle de rejeter $H_0: \mu = \mu_0$ au profit de $H_1: \mu \neq \mu_0$ si

\[\begin{equation} z_0 < z_{\alpha/2} \text{ ou si } z_0 > z_{1-\alpha/2} \tag{5.1} \end{equation}\]

et de na pas rejeter $H_0$ si

\[\begin{equation} z_{\alpha/2} \leq z_0 \leq z_{1-\alpha/2} \tag{5.2} \end{equation}\]

L’équation (5.1) définit la région critique ou de rejet de $H_0$. La probabilité de l’erreur de première espèce de cette procédure du test est $\alpha$. On peut déduire de l’équation (5.2) que les deux valeurs critique de la figure 5.1 sont les suivantes:

\[ v_1 = \mu_0 + z_{\alpha/2} \, \sigma/\sqrt{n} \quad \text{ et } \quad v_2 = \mu_0 + z_{1-\alpha/2} \, \sigma/\sqrt{n} \]

Exemple 5.2 On étudie la vitesse de combustion du carburant d’une fusée. Le cahier des charges exige que la vitesse moyenne de combustion soit de $40\, cm/{s}$. Supposons que l’écart-type de la vitesse de combustion est d’environ $2 \, cm/s$ et que cette variable suit une distribution normale.

Hypothèses et seuil: L’expérimentateur décide de spécifier une probabilité d’erreur de première espèce $\alpha=0.05$ et base le test sur un échantillon aléatoire de taille $n=25$. Il veut tester les hypothèses ${H}_{0}: \mu=40\, cm/s$ contre ${H}_{1}: \mu \neq 40\, cm/s$.
Règle de rejet de ${H}_{0}$: Puisque le test est bilatéral, on rejettera $H_{0}$ si $\overline{x}$ est trop grand ou trop petit par rapport à $40\, cm/s$. On devra comparer la valeur observée $z_{0}$ de la statistique du test $Z_{0}$ avec les valeurs critiques $\pm z_{0.025}=\pm 1,96$. Si $-1.96 \leq z_{0} \leq 1.96$, l’hypothèse nulle ne sera pas rejetée.
Calcul de la statistique observée: Les 25 unités sont essayées, et la vitesse moyenne de combustion de l’échantillon obtenue est $\overline{x}=41.25\, cm/s$. La valeur de la statistique dans l’équation $Z_0$ est

\[ z_{0}=\frac{\overline{x}-\mu_{0}}{\sigma / \sqrt{n}}=\frac{41.25-40}{2 / \sqrt{25}}=3.125 \]

Décision: On remarque que $z_0$ appartient à la région critique, car $3.125>1.96$. Donc, $H_0$ est rejetée.
Conclusion: La vitesse moyenne de combustion excède $40\, cm/s$ de façon significative au seuil de $5 \%$.

5.2.1.2 La procédure pour les tests unilatéraux

Supposons maintenant qu’on désire tester l’hypothèse alternative unilatérale à droite, soit

\[ H_{0}: \mu=\mu_{0} \text { contre } H_{1}: \mu > \mu_{0} \]

En définissant la région critique de ce test, on remarque qu’une valeur négative de la statistique $Z_0$ ne conduira jamais à conclure que $H_0: \mu=\mu_0$ est fausse. On doit donc placer la région critique dans l’aile supérieure de la distribution $\mathcal{N}(0,1)$ et rejeter $H_0$ pour les trop grandes valeurs de $z_0$. Autrement dit, on doit rejeter $H_0$ si $z_0 > z_{1-\alpha}$.

De même, pour tester l’hypothèse unilatérale à gauche

\[ H_{0}: \mu=\mu_{0} \text { contre } H_{1}: \mu < \mu_{0} \] on doit calculer la statistique $Z_0$ et rejeter $H_0$ pour les trop petites valeurs de $z_0$. Autrement dit, la région critique est dans l’aile inférieure de la distribution $\mathcal{N}(0,1)$, et on rejette $H_0$ si $z_0 < z_{\alpha}$

#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'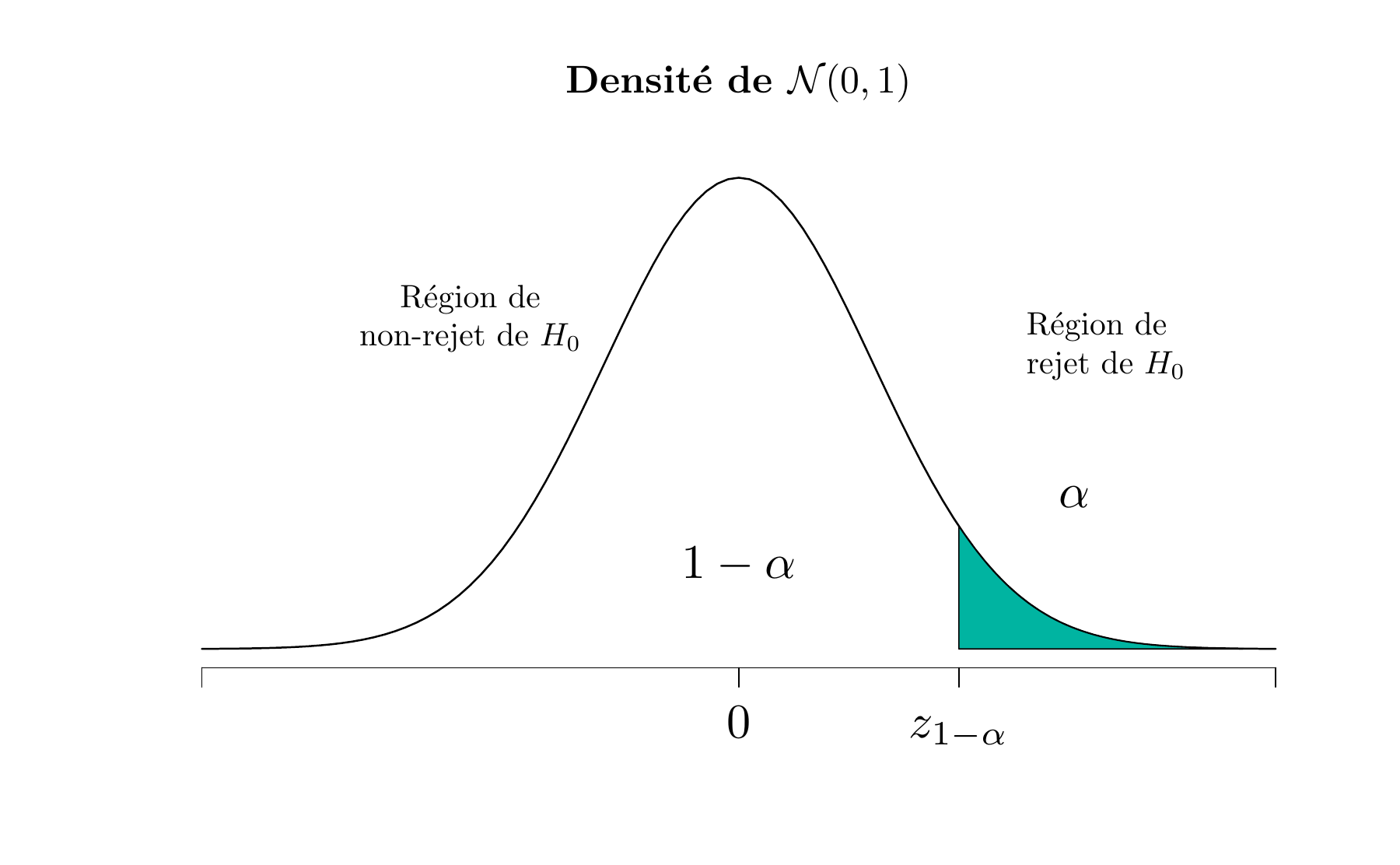

$La distribution de $Z_0$ lorsque $H_0 : \mu = \mu_0$ est vraie contre $H_1: \mu > \mu_0$ (**Upper-tailed test**)$

Figure 5.3: La distribution de $Z_0$ lorsque $H_0 : \mu = \mu_0$ est vraie contre $H_1: \mu > \mu_0$ (Upper-tailed test)

#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'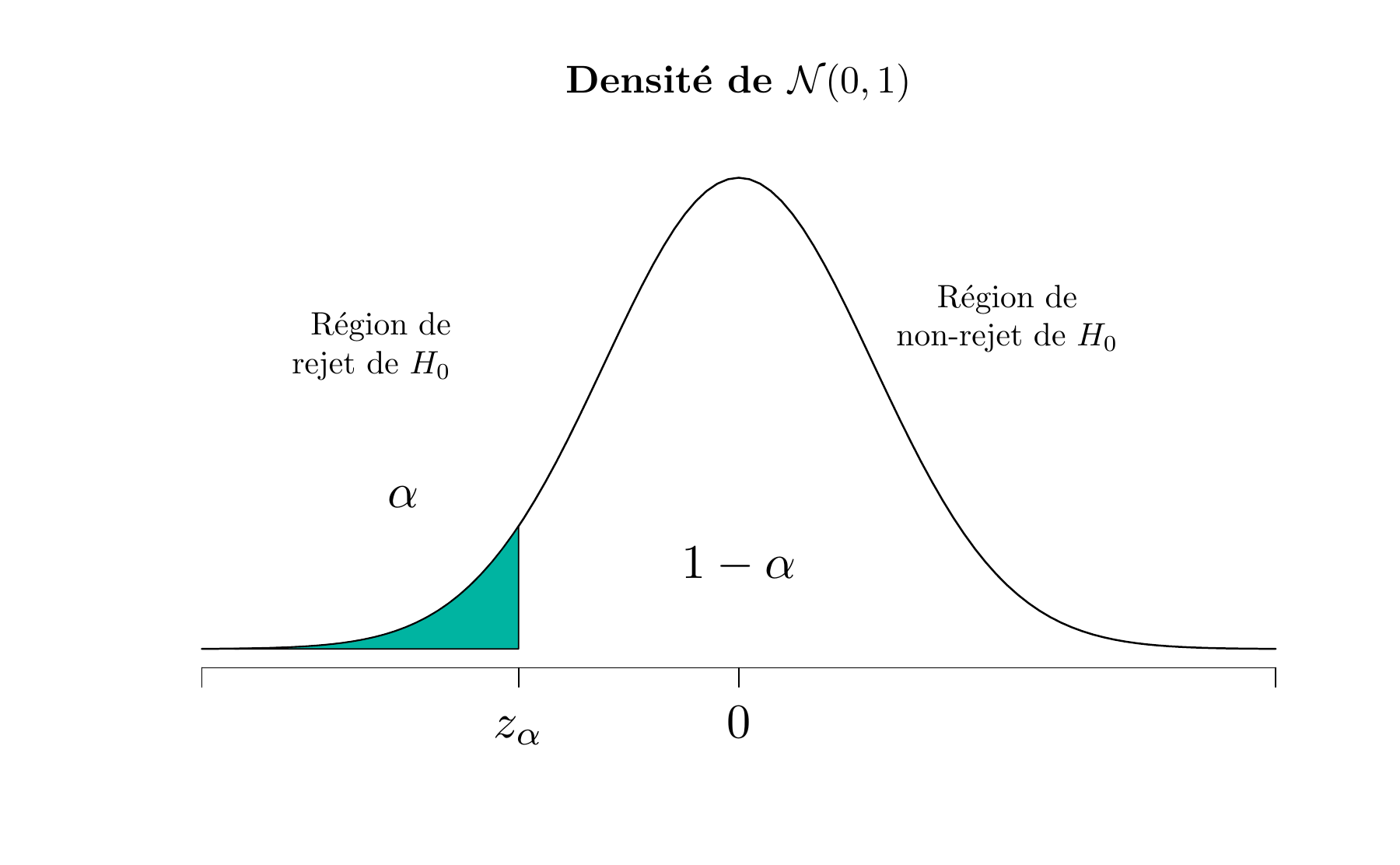

$La distribution de $Z_0$ lorsque $H_0 : \mu = \mu_0$ est vraie contre $H_1: \mu < \mu_0$ (**Lower-tailed test**)$

Figure 5.4: La distribution de $Z_0$ lorsque $H_0 : \mu = \mu_0$ est vraie contre $H_1: \mu < \mu_0$ (Lower-tailed test)

5.2.1.3 Le calcul du risque de deuxième espèce et la puissance du test

Lorsque l’analyste teste des hypothèses, il choisit directement la probabilité de l’erreur de première espèce $\alpha$. Cependant, la probabilité de l’erreur de deuxième espèce $\beta$ doit aussi être prise en compte.

Considérons par exemple l’hypothèse unilatérale:

\[ H_{0}: \mu=\mu_{0} \text { contre } H_{1}: \mu > \mu_{0} \] Supposons que l’hypothèse nulle est fausse et que la valeur réelle de la moyenne est $\mu_1$, une valeur plus grande que $\mu_0$. Puisque $H_1$ est vraie, la moyenne échantillonnale $\overline{X}$ suit la loi $\mathcal{N}(\mu_1,\sigma^2/n)$. La figure 5.5 représente la distribution de $\overline{X}$ sous l’hypothèse nulle $H_0$ et sous l’hypothèse alternative $H_1$. On rejette $H_0$ si $\overline{x}$ est supérieure à la valeur critique $v$, qui vaut $\mu_0 + z_{1-\alpha} \sigma/\sqrt{n}$. Rappelons qu’une erreur de deuxième espèce est commise si $H_0$ n’est pas rejetée alors qu’elle est fausse. L’examen de cette figure révèle que si $H_1$ est vraie, une erreur de deuxième espèce ne sera commise que si $\overline{x} < v$. Autrement dit, la probabilité de l’erreur de deuxième espèce $\beta$ correspond à la région verte de la figure 5.5.

#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'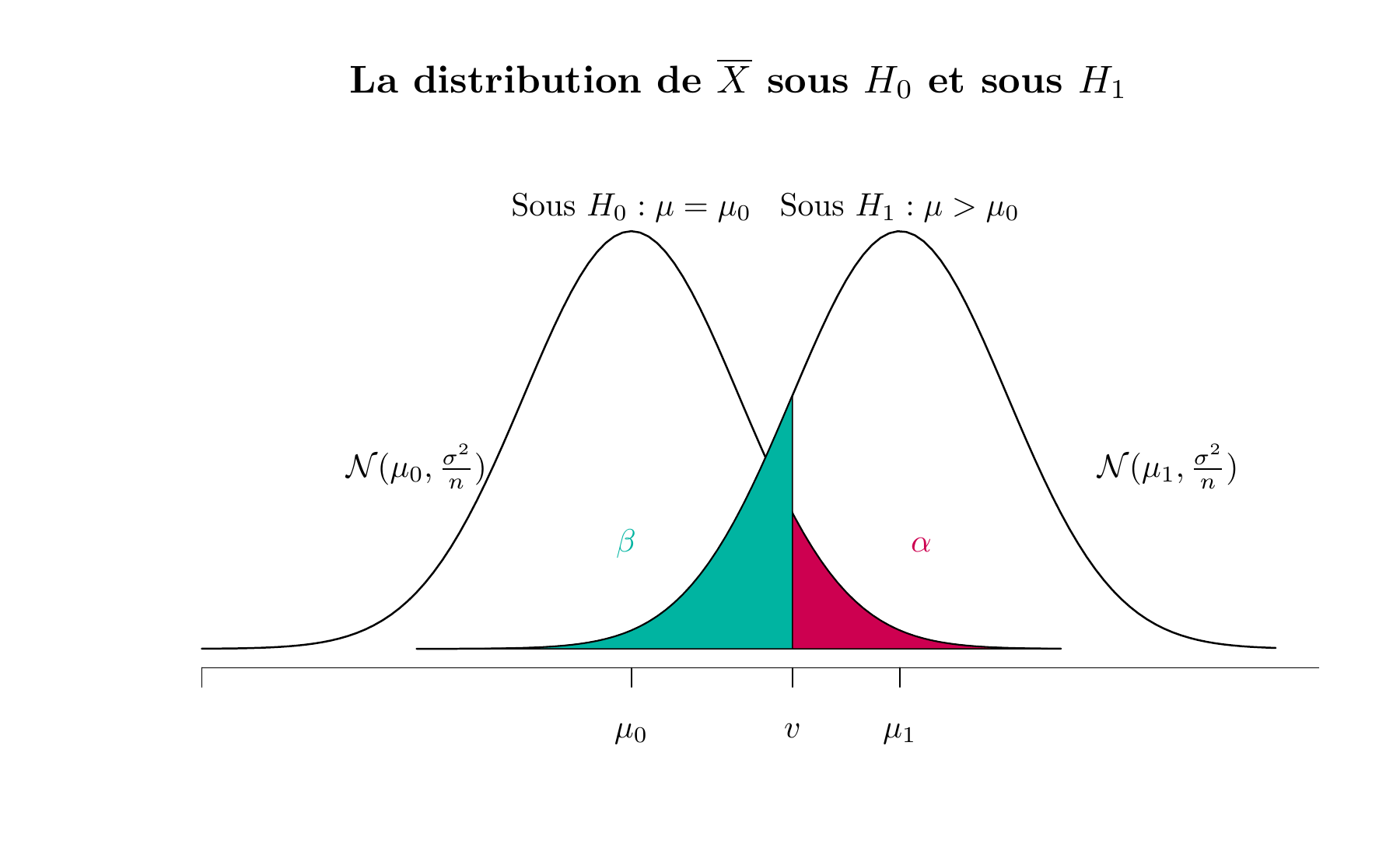

$La distribution de $\overline{X}$ sous $H_0$ et sous $H_1$$

Figure 5.5: La distribution de $\overline{X}$ sous $H_0$ et sous $H_1$

#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'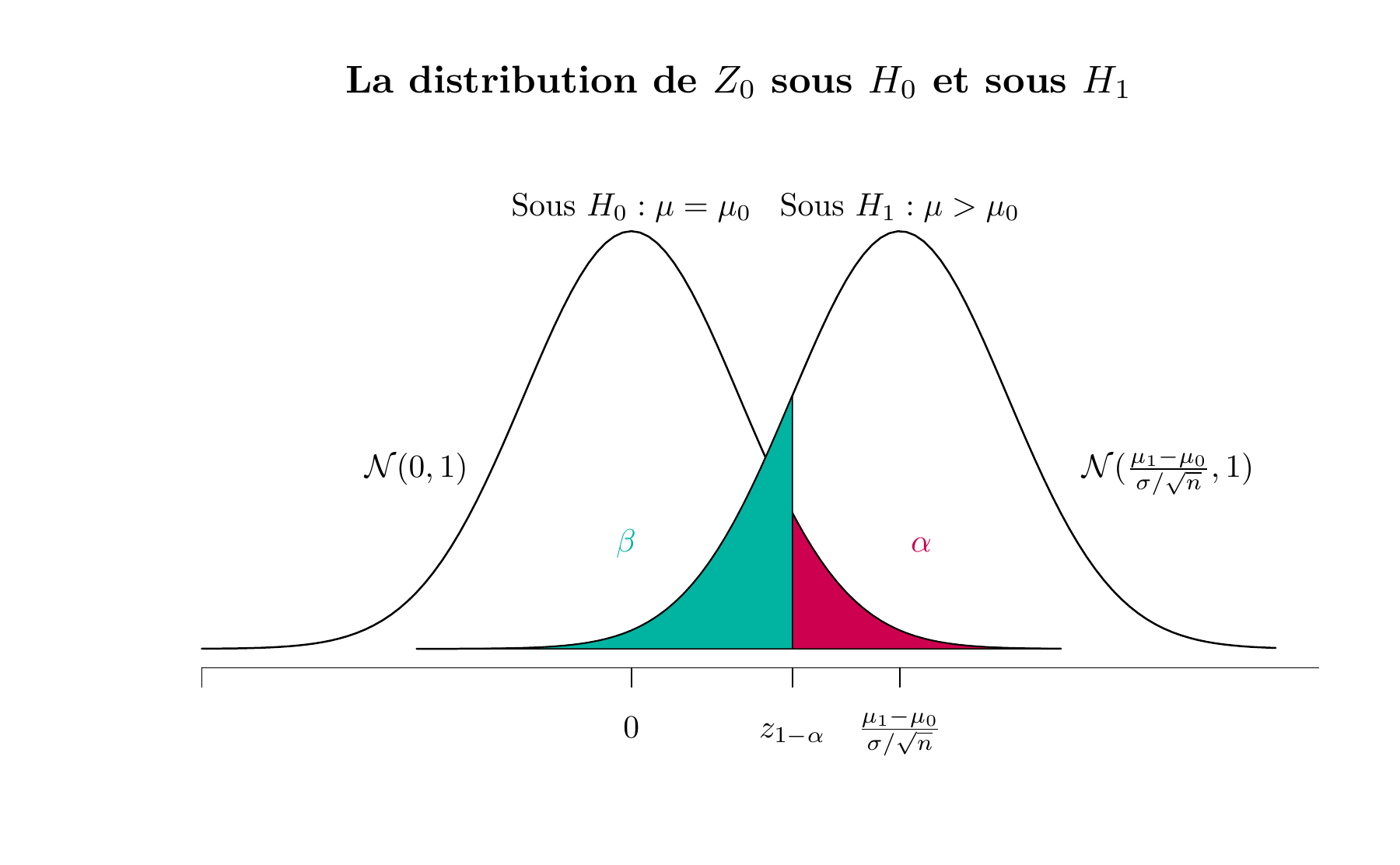

Figure 5.6: La distribution de $Z_0$ sous $H_0$ et sous $H_1$

Les facteurs qui influencent le risque de deuxième espèce $\beta$ du test sur une moyenne:

$\beta$ diminue lorsque $\mu_1$ s’éloigne de $\mu_0$.
$\beta$ diminue lorsque $n$ augmente.
$\beta$ diminue lorsque $\alpha$ augmente.

Concernant la puissance du test, qui vaut $1 - \beta$:

La puissance d’un test est fonction de la nature de $H_1$, un test unilatéral est plus puissant qu’un test bilatéral.
La puissance d’un test augmente lorsque $n$ augmente.
La puissance d’un test diminue lorsque $\alpha$ diminue.

Considérons le problème du combustible de fusée de l’exemple 5.2 et tenons pour acquis qu’on réalise un test unilatérale à droite: \[ H_{0}: \mu=40\, cm/{s} \text { contre } H_{1}: \mu > 40 \, cm/{s} \] Supposons que l’analyste veut rejeter $H_0$ avec une forte probabilité si la véritable vitesse moyenne de combustion est $\mu=41\, cm/{s}$. En d’autres termes, il veut une faible probabilité d’erreur de deuxième espèce si $\mu=41\, cm/{s}$. Montrer que la puissance du test est égale à $80.5\%$.

Indication: Commencer par calculer: \[\beta = P(\text{Ne pas rejeter } H_0 | H_1 \text{ est vraie})\]

Puisque la puissance du test est affectée par la taille de l’échantillon, il est courant de fixer $1-\beta$ et de trouver la valeur de $n$ qui nous permet de l’atteindre.

5.2.2 Les tests sur la moyenne d’une distribution normale de variance inconnue

On a élaboré la procédure de test pour l’hypothèse nulle $H_0:\mu=\mu_0$ en supposant que la variance $\sigma^2$ est connue. Cependant, dans de nombreuses situations pratiques, $\sigma^2$ n’est pas connue. Pour tester des hypothèses sur la moyenne $\mu$ d’une population lorsque la variance $\sigma^2$ est inconnue, on suppose que la distribution de la variable $X$ est normale¹². Cette supposition mène à une procédure de test souvent appelée test $t$ ou test de Student, car elle fait appel à la loi de Student¹³.

5.2.2.1 La procédure pour le test bilatéral

Supposons que $X$ est une variable aléatoire de distribution normale de moyenne $\mu$ et de variance $\sigma^{2}$ inconnues. Testons l’hypothèse que $\mu$ est égale a une constante $\mu_{0}$. On remarque que cette situation est similaire à celle qui a été traitée dans la section précédente sauf que, maintenant, les deux paramètres $\mu$ et $\sigma^{2}$ sont inconnus. Supposons qu’on dispose d’un échantillon de taille $n$, soit $X_{1}, X_{2}, \ldots, X_{n}$, et soit respectivement $\overline{X}$ et ${S_n^{*}}^2=\frac{n}{n-1} S_{n}^{2}$ la moyenne et la variance de l’échantillon.

Supposons qu’on désire tester l’hypothèse alternative bilatéral

\[ {H}_{0}: \mu=\mu_{0} \text{ contre } {H}_{1}: \mu\neq \mu_{0} \]

La procédure du test $t$ repose sur la statistique

\[ T_{0}=\frac{\overline{X}-\mu_{0}}{S^* / \sqrt{n}} \] qui suit la loi $St$ avec $n-1$ degrés de liberté si l’hypothèse nulle ${H}_{0}: \mu=\mu_{0}$ est vraie.

Critère de rejet de $H_0: \mu = \mu_0$ (test bilatéral, loi normale, variance inconnue)

On se donne comme règle de rejeter $H_0: \mu = \mu_0$ au profit de $H_1: \mu \neq \mu_0$ si

\[|t_0| > t_{n-1,1-\frac{\alpha}{2}}\]

où $t_0$ est la valeur observée de la Statistique $T_0$ et $t_{n-1,1-\frac{\alpha}{2}}$ est le quantile d’ordre $1-\alpha/2$ de la loi $t$ de Student avec $n-1$ degrés de liberté.

5.2.2.2 La procédure pour les tests unilatéraux

Pour l’hypothèse alternative unilatérale à droite

\[ H_{0}: \mu=\mu_{0} \text { contre } H_{1}: \mu > \mu_{0} \] On calcule la valeur observée $t_0$ et on rejette $H_0$ si $t_0 > t_{n-1,{1-\alpha}}$.

Pour l’hypothèse alternative unilatérale à gauche

\[ H_{0}: \mu=\mu_{0} \text { contre } H_{1}: \mu < \mu_{0} \] On rejette $H_0$ si $t_0 < t_{n-1,{\alpha}}$.

Les tests sur la moyenne dans s’effectuent à l’aide de la fonction t.test()

5.2.3 Les tests sur la variance d’une distribution normale

Soit un $n$-échantillon $\left(X_{1}, \ldots, X_{n}\right)$ issu d’une population de loi normale, de moyenne $\mu$ et de variance $\sigma^{2}$. La normalité est indispensable pour ce test sur la variance.

5.2.3.1 La procédure pour le test bilatéral

Supposons qu’on désire tester l’hypothèse que la variance $\sigma^2$ d’une distribution normale est égale à une valeur spécifiée $\sigma_0^2$, on teste

\[ H_{0}: \sigma^2=\sigma_{0}^2 \text { contre } H_{1}: \sigma^2 \neq \sigma_{0}^2 \] On utilisera la statistique

\[ U_0 = \frac{(n-1) {S_n^{*}}^2}{\sigma_{0}^2} \]

où ${S_n^{*}}^2$ est la variance corrigée de l’échantillon. Si $H_0:\sigma^2=\sigma_{0}^2$ est vraie, alors la statistique $U_0$ suit la loi du $\chi^2(n-1)$.

Critère de rejet de $H_0:\sigma^2=\sigma_{0}^2$ (test bilatéral, loi normale)

On rejette $H_0:\sigma^2=\sigma_{0}^2$ si

\[u_0 < \chi^2_{n-1,\frac{\alpha}{2}} \quad \text{ ou } \quad u_0 > \chi^2_{n-1,1-\frac{\alpha}{2}}\]

où $u_0$ est la valeur observée de la Statistique $U_0$, $\chi^2_{n-1,\frac{\alpha}{2}}$ et $\chi^2_{n-1,1-\frac{\alpha}{2}}$ sont les quantile d’ordre $\alpha/2$ et $1-\alpha/2$ de la loi $\chi^2$ avec $n-1$ degrés de liberté.

#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'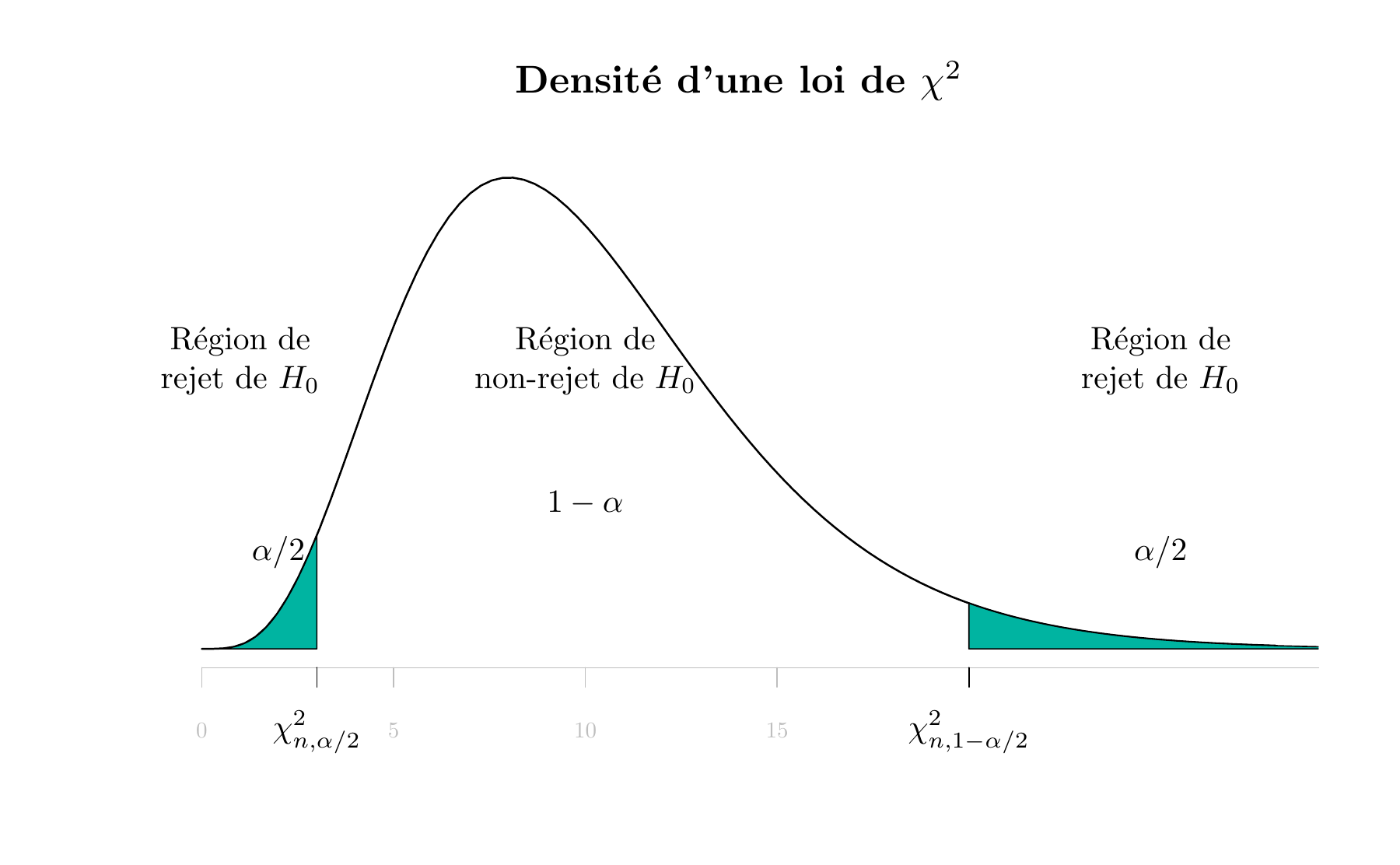

$La distribution de $U_0$ lorsque $H_0 : \sigma^2 = \sigma^2_0$ est vraie$

Figure 5.7: La distribution de $U_0$ lorsque $H_0 : \sigma^2 = \sigma^2_0$ est vraie

Attention, contrairement à la loi de Student et la loi normale centrée réduite, la densité de la loi du $\chi^2$ n’est pas symétrique.

5.2.3.2 La procédure pour les tests unilatéraux sur la variance

Pour l’hypothèse alternative unilatérale à droite

\[ H_{0}: \sigma^2=\sigma^2_{0} \text { contre } H_{1}: \sigma^2> \sigma^2_{0} \] On calcule la valeur observée $u_0$ et on rejette $H_0$ si $u_0 > \chi^2_{n-1,1-\alpha}$.

Pour l’hypothèse alternative unilatérale à gauche

\[ H_{0}: \sigma^2=\sigma^2_{0} \text { contre } H_{1}: \sigma^2< \sigma^2_{0} \] On rejette $H_0$ si $u_0 < \chi^2_{n-1,\alpha}$.

5.2.4 Les tests sur une proportion

Dans la population étudiée, une proportion $p$ des individus possèdent un certain caractère $C$. On se propose de comparer cette proportion $p$ à une valeur de référence $p_0$. On considère un échantillon d’individus de taille $n$ de cette population. La variable aléatoire $X_i$ égale à $1$ si l’individu $i$ possède le caractère $C$ suit une loi de Bernoulli $\mathcal{B}(p)$. Si $n$ est suffisamment grand, on peut considérer que $\sum_{i=1}^n X_i$ suit une loi normale $\mathcal{N}(np,np(1-p))$, d’où la fréquence empirique $\hat{p}_n= \frac{1}{n}\sum_{i=1}^n X_i$ suit une loi normale $\mathcal{N}(p,\frac{p(1-p)}{n})$.

Supposons qu’on désire tester

\[ H_0: p = p_0 \text { contre } H_1: p \neq p_0 \]

La statistique du test est donc la fréquence empirique $\hat{p}_n$ qui suit sous $H_0$ la loi $\mathcal{N}(p_0,\frac{p_0(1-p_0)}{n})$.

Pour tester $H_0: p = p_0$ on calcule la statistique du test

\[ Z_0 = \frac{\hat{p}_n - p_0}{\sqrt{ \frac{p_0(1-p_0)}{n}}} \] qui suit approximativement la loi $\mathcal{N}(0,1)$ si l’hypothèse nulle est vraie.

Critère de rejet de $H_0:p = p_0$ (test bilatéral, grand échantillon)

On rejette $H_0:p = p_0$ si

\[|z_0| > z_{1-\alpha/2}\] où $z_{1-\alpha/2}$ est le quantile d’ordre $1-\alpha/2$ de la loi $\mathcal{N}(0,1)$.

On situe comme d’habitude les régions critiques des hypothèses alternatives unilatérales.

Il y a dualité entre intervalles de confiance et tests d’hypothèses↩︎
ou comparer la valeur $p$ (p-value) avec le seuil du test. Cette valeur corresponds à une probabilité. Si cette probabilité est inférieure à $\alpha$, on rejette $H_0$. Si elle est supérieure à $\alpha$, on ne rejette pas $H_0$.↩︎
supposition raisonnable dans de nombreux cas↩︎
Si la supposition est déraisonnable, on peut spécifier une autre loi (exponentielle, Weibull, etc..) et utiliser une méthode générale de construction de test pour obtenir une procédure valide, ou on peut utiliser un des tests non paramétriques qui sont valides pour toute distribution.↩︎

Décision \(\backslash\) Vérité	\(H_0\)	\(H_1\)
\(H_0\)	conclusion correcte	erreur de deuxième espèce
\(H_1\)	erreur de première espèce	conclusion correcte

Décision \(\backslash\) Vérité	\(H_0\)	\(H_1\)
\(H_0\)	niveau de confiance \(1-\alpha\)	risque \(\beta\)
\(H_1\)	risque \(\alpha\)	Puissance de test \(1-\beta\)