Chapitre 4 Estimation par Intervalle de confiance
Jusqu’à présent, on a estimé un paramètre \(\theta\) par une unique valeur \(\hat{\theta}_{n}\) (estimation ponctuelle). Si l’estimateur \(\hat{\theta}_{n}\) possède de bonnes propriétés (sans biais, variance minimale), on peut s’attendre à ce que \(\hat{\theta}_{n}\) soit proche de la vraie valeur de \(\theta\). Cependant, il est très peu probable que \(\hat{\theta}_{n}\) soit exactement égal à \(\theta\). En particulier, si la loi de \(\hat{\theta}_{n}\) est continue, on est certains que \(P\left(\hat{\theta}_{n}=\theta\right)=0\)
Par conséquent, plutôt que d’estimer \(\theta\) par la seule valeur \(\hat{\theta}_{n}\), il semble raisonnable de proposer un ensemble de valeurs vraisemblables pour \(\theta,\) qu’il est logique de prendre proches de \(\hat{\theta}_{n}\). Cet ensemble de valeurs est appelé région de confiance. Dire que toutes les valeurs de cet ensemble sont vraisemblables pour \(\theta\), c’est dire qu’il y a une forte probabilité que \(\theta\) appartienne à cet ensemble.
On supposera dans ce chapitre que \(\theta \in \mathbb{R}\), donc la région de confiance sera un intervalle.
\(\alpha\) est la probabilité que le paramètre \(\theta\) n’appartienne pas à l’intervalle \(I\), c’est à dire la probabilité que l’on se trompe en affirmant que \(\theta \in I\). C’est donc une probabilité d’erreur, qui doit être assez petite. Les valeurs usuelles de \(\alpha\) sont \(10 \%, 5 \%, 1 \%,\) etc.
Remarque fondamentale: Les intervalles de confiance suscitent souvent des erreurs d’interprétation et des abus de langage. La raison essentielle de ce problème est expliquée ci dessous.
Dans l’écriture \(P(\theta \in I)\), \(\theta\) est une grandeur inconnue mais non aléatoire. Ce sont les bornes de l’intervalle \(I\) qui sont aléatoires. Posons \(I=[Z_1,Z_2]\). \(Z_1\) et \(Z_2\) sont des variables aléatoires. Soient \(z_1\) et \(z_2\) les réalisations de \(Z_1\) et \(Z_2\) pour une expérience donnée. Il est correct de dire une phrase du type : “\(\theta\) a \(95 \%\) de chances d’être compris entre \(Z_1\) et \(Z_2\)”, mais il est incorrect de dire: “\(\theta\) a \(95 \%\) de chances d’être compris entre \(z_1\) et \(z_2\)”. En fait, si on recommence 100 fois l’expérience, on aura 100 réalisations du couple \(\left(Z_{1}, Z_{2}\right)\), et donc 100 intervalles de confiance différents. En moyenne, \(\theta\) sera dans 95 de ces intervalles.
Par conséquent, il vaut mieux dire : “on a une confiance de \(95 \%\) dans le fait que \(\theta\) soit compris entre \(z_1\) et \(z_2\)”.
Le problème à régler est de trouver un procédé pour déterminer un intervalle de confiance pour un paramètre \(\theta\). Il semble logique de proposer un intervalle de confiance centré sur un estimateur performant \(\hat{\theta}_{n},\) c’est-à-dire de la forme \(I=\left[\hat{\theta}_{n}-\varepsilon, \hat{\theta}_{n}+\varepsilon\right]\) . Il reste alors à déterminer \(\varepsilon\) de sorte que :
\[ P(\theta \in I)=P\left(\hat{\theta}_{n}-\varepsilon \leq \theta \leq \hat{\theta}_{n}+\varepsilon\right)=P\left(\left|\hat{\theta}_{n}-\theta\right| \leq \varepsilon\right)=1-\alpha \]
Si cet intervalle de confiance est petit, l’ensemble des valeurs vraisemblables pour \(\theta\) est resserré autour de \(\hat{\theta}_{n}\). Si l’ntervalle de confiance est grand, des valeurs vraisemblables pour \(\theta\) peuvent être éloignées de \(\hat{\theta}_{n}\). Donc un intervalle de confiance construit à partir d’un estimateur permet de mesurer la précision de cet estimateur.
Soit \(a\) et \(b\) les bornes d’un intervalle de confiance \(I C_{1-\alpha}(\theta)\) de niveau de confiance \(1-\alpha\) pour le paramètre \(\theta\). On a:
\[ p(a \leq \theta \leq b)=1-\alpha \text { et donc } p(\theta<a)+p(\theta>b)=\alpha \] En posant \(\alpha=\alpha_{1}+\alpha_{2}\), il existe une infinité de choix possibles pour \(\alpha_{1}\) et \(\alpha_{2}\), et donc de choix pour \(a\) et \(b\). Nous ne considérons que le cas d’un intervalle bilatéral à risques symétriques, pour lesquels le risque est partagé en deux parts égales \(\alpha_{1}=\alpha_{2}=\frac{\alpha}{2}\). Néanmoins il arrive en pratique que l’on s’intéresse à des risques unilatéraux, mais nous en parlerons plus en détail dans les chapitres suivants sur les tests statistiques.
Pour trouver un intervalle de confiance, il existe plusieurs méthodes. La plus efficace consiste à chercher une fonction pivotale, c’est à dire une variable aléatoire fonction à la fois du paramètre \(\theta\) et des observations \(X_{1}, \ldots, X_{n}\), dont la loi de probabilité ne dépende pas de \(\theta\). Dans la suite de ce chapitre, nous allons illustrer cette méthodologie par des exemples, en déterminant des intervalles de confiance pour:
- La moyenne et la variance dans un échantillon de loi normale.
- Une proportion, c’est-à-dire le paramètre d’un échantillon de loi de Bernoulli.
Remarques:
- L’intervalle de confiance est fonction de l’estimation \(\hat{\theta}_{n}\) de \(\theta\).
- L’intervalle de confiance est également fonction de \(\alpha\). Plus \(\alpha\) est petit, plus le niveau de confiance est grand, et donc plus l’intervalle s’élargit.
- Lorsque la taille de l’échantillon grandit, l’estimateur \(\hat{\theta}_{n}\) étant convergeant la variance \(V(\hat{\theta}_{n})\) diminue, et l’intervalle se rétrécit.
Il est recommandé avant de poursuivre la lecture de se rappeler des lois déduites de la loi normale: loi de \(\chi^{2}\), loi de Student \(St(n)\) et loi de Fisher-Snedecor \(\mathcal{F}(n,m)\).
Suite à la définition de ces lois, nous introduisons le théorème de Fisher:
Théorème 4.1 \iffalse (Théorème de Fisher) Si \(X_{1}, \ldots, X_{n}\) sont indépendantes et de même loi \(\mathcal{N}\left(m, \sigma^{2}\right)\), alors, en posant \(\overline{X}_{n}=\frac{1}{n} \sum_{i=1}^{n} X_{i}\) et \(S_{n}^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\overline{X}_{n}\right)^{2}\), on a:
- \(\sum_{i=1}^{n} X_{i}\) est de loi \(\mathcal{N}\left(n m, n \sigma^{2}\right)\).
- \(\overline{X}_{n}\) est de loi \(\mathcal{N} \left(m, \frac{\sigma^{2}}{n}\right)\).
- \(\frac{1}{\sigma^{2}} \sum_{i=1}^{n}\left(X_{i}-m\right)^{2}\) est de loi \(\chi_{n}^{2}\).
- \(\frac{1}{\sigma^{2}} \sum_{i=1}^{n}\left(X_{i}-\overline{X}_{n}\right)^{2}=\frac{n S_{n}^{2}}{\sigma^{2}}\) est de loi \(\chi_{n-1}^{2}\).
- \(\overline{X}_{n}\) et \(S_{n}^{2}\) sont indépendantes.
- \(\sqrt{n-1} \frac{\overline{X}_{n}-m}{S_{n}}\) est de loi de Student \(S t(n-1)\).
4.1 Intervalles de confiance pour les paramètres de la loi normale
4.1.1 Intervalle de confiance pour l’espérance d’une loi normale avec variance connue
Soit \(X \sim \mathcal{N}\left(\mu, \sigma^{2}\right)\) avec \(\sigma\) connu. Le meilleur estimateur de \(\mu\) est \(\overline{X}\). Comme \(X\) est de loi normale on a
\[ Z=\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}} \sim \mathcal{N}(0,1) \] En prenant des risques symétriques, on peut lire dans les tables les quantiles \(z_\frac{\alpha}{2}\) et \(z_{1-\frac{\alpha}{2}}\) de la loi normale centrée réduite d’ordres respectifs \(\frac{\alpha}{2}\) et \(1-\frac{\alpha}{2}\), tels que :
\[ P\left(z_{\frac{\alpha}{2}} \leq Z \leq z_{1-\frac{\alpha}{2}}\right)=1-\alpha \] ou encore \[ P\left(Z \leq z_{\frac{\alpha}{2}}\right)=p\left(Z \geq z_{1-\frac{\alpha}{2}}\right)=\frac{\alpha}{2} \] Les quantiles
La notion du quantile est définie de la façon suivante:
Ces quantiles sont notés de différentes façons: \(z_{\alpha}\) pour la loi normale, \(t_{n,\alpha}\) pour la loi de Student à \(n\) degrés de liberté, \(z_{n,\alpha}\) pour la loi de \(\chi_{n}^{2}\), etc.
La figure 4.1 suivante illustre la définition de ces quantiles:
#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'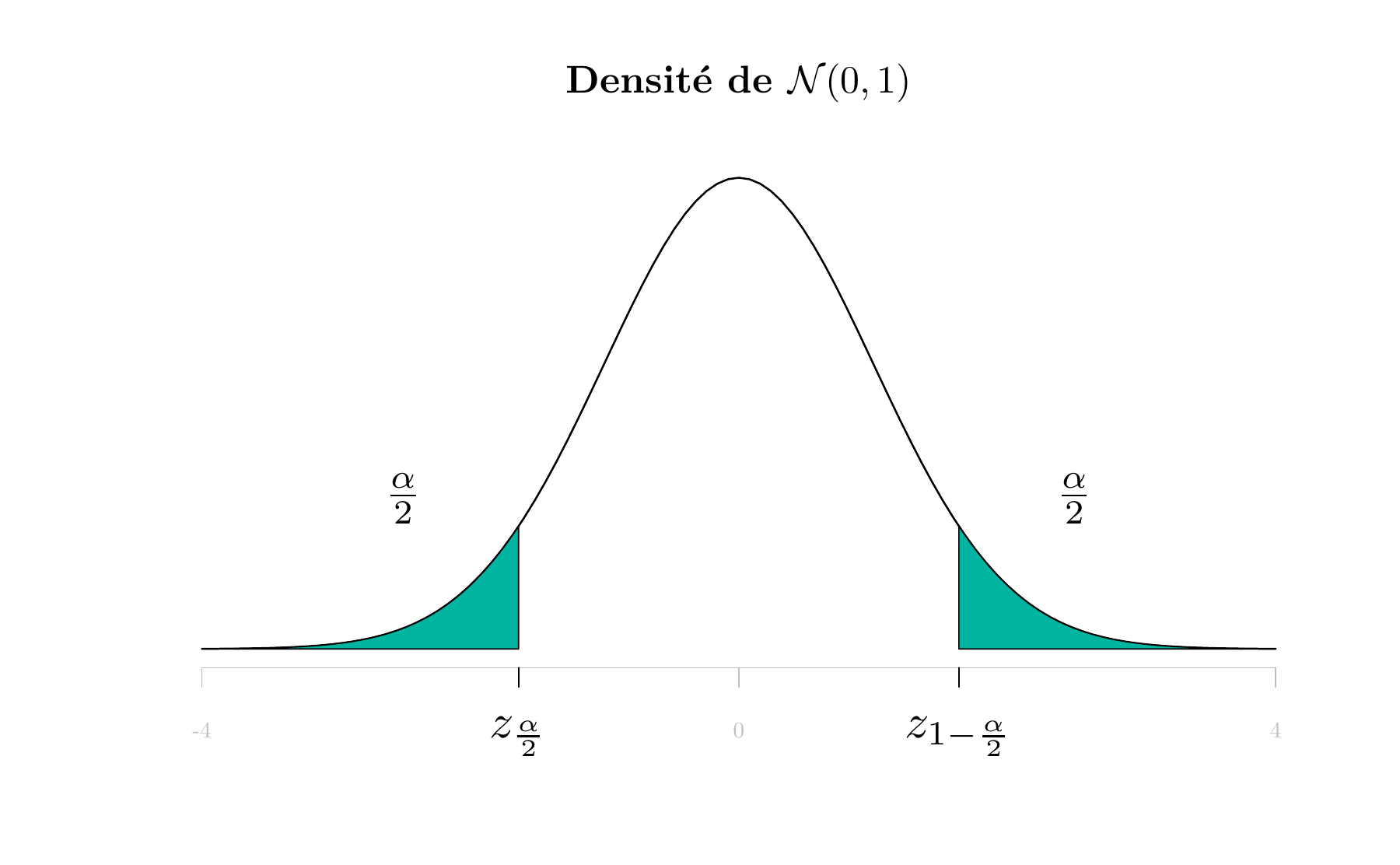
Figure 4.1: Quantiles \(z_{\frac{\alpha}{2}}\) et \(z_{1-\frac{\alpha}{2}}\) de la loi normale centrée réduite
Comme la loi normale est symétrique, on a la propriété suivante:
\[z_{1-\frac{\alpha}{2}} = - z_{\frac{\alpha}{2}}\] Ces quantiles sont donnés par les tables statistiques. Par exemple, pour \(\alpha=0.05=5\%\), on obtient \(z_{\frac{\alpha}{2}}=-1.96\).
Pour \(\alpha=0.05=5\%\), on obtient selon la table de la loi normale centrée réduite \(z_{\frac{\alpha}{2}}=-1.96\) et \(z_{1-\frac{\alpha}{2}} = 1.96\).
Revenons à la détermination d’IC pour l’espérance d’une loi normale avec variance connue, on a
\[P(z_{\frac{\alpha}{2}} \leq Z \leq z_{1-\frac{\alpha}{2}}) = 1- \alpha\]
qui peut s’écrire
\[P(z_{\frac{\alpha}{2}} \leq Z \leq -z_{\frac{\alpha}{2}}) = 1- \alpha\] d’où on tire
\[P(\overline{X} + z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} \leq \mu \leq \overline{X} - z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}) = 1- \alpha\]
D’où l’intervalle de confiance:
\[I C_{1-\alpha}(\mu)= [\overline{X} + z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}},\overline{X} - z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}]\]
Pour une réalisation numérique \(x_1,\ldots,x_n\) d’un échantillon \(X_1,\ldots,X_n\) de taille \(n\), on obtient l’intervalle de confiance sur \(\hat{\mu}\) au niveau de confiance \(1-\alpha\):
\[I C_{1-\alpha}(\mu)= [\overline{x} + z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}},\overline{x} - z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}]\] qui donne pour \(\alpha=0.05\):
\[[\overline{x} - 1.96 \frac{\sigma}{\sqrt{n}},\overline{x} +1.96 \frac{\sigma}{\sqrt{n}}]\]
La table de la loi normale centrée réduite et une application interactive permettant de calculer les quantiles de loi normale se trouvent dans l’annexe B. Une deuxième table qui donne directement le quantile \(z_{1-\frac{\alpha}{2}}\) par rapport à \(\alpha\) est présentée dans l’annexe C.
Le problème est que cet intervalle n’est utilisable que si on connaît la valeur de \(\sigma\). Or, dans la pratique, on ne connaît jamais les vraies valeurs des paramètres. Une idée naturelle est alors de remplacer \(\sigma\) par un estimateur.
4.1.2 Intervalle de confiance pour l’espérance d’une loi normale avec variance inconnue
Si la variance \(\sigma^2\) est inconnue, on utilisera à sa place son meilleur estimateur \(S_n^{*2}\). Selon le théorème de Fisher, on sait que \(\frac{n }{\sigma^{2}}S_{n}^{2}\) est de loi \(\chi_{n-1}^{2}\), et que \(\frac{n-1}{\sigma^{2}} S_{n}^{*2}\) est de loi \(\chi_{n-1}^{2}\) aussi.
La statistique que l’on utilisera est donc
\[T_{n-1} = \frac{\overline{X}-\mu}{S_n^*/\sqrt{n}}\]
En remarquant qu’elle s’écrit
\[T_{n-1} = \displaystyle \frac{\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}}{\sqrt{\frac{\frac{n-1}{\sigma^2}S^{*2}}{n-1}}}\] on trouve qu’elle suit une loi de Student à \(n-1\) degrés de liberté, comme rapport d’une loi normale centrée réduite sur la racine d’un \(\chi^2\) divisé par son degré de liberté.
Comme précédemment, on obtient l’intervalle de confiance:
\[I C_{1-\alpha}(\mu)= [\overline{x} + t_{n-1,\frac{\alpha}{2}} \frac{S^*}{\sqrt{n}},\overline{x} - t_{n-1,\frac{\alpha}{2}} \frac{S^*}{\sqrt{n}}]\] où \(t_{n-1,\frac{\alpha}{2}}\) est le quantile d’ordre \(\frac{\alpha}{2}\) de la loi de Student à \(n-1\) degrés de liberté.
Une table de la loi de Student se trouve dans l’annexe D.
Remarque: La variable aléatoire \(\frac{\overline{X}-\mu}{S^*/\sqrt{n}}\) est une fonction des observations \(X_1,\ldots,X_n\) et du paramètre \(\mu\) pour lequel on recherche un intervalle de confiance, dont la loi de probabilité ne dépend pas des paramètres du modèle \(\mu\) et \(\sigma^2\). C’est ce qu’on a appelé une fonction pivotale et c’est ce que nous utiliserons pour construire des intervalles de confiance.
Si la loi de \(X\) n’est pas une loi normale: Dans ce cas, lorsque la taille de l’échantillon \(n\) est supérieure ou égale à 30, le théorème central limite nous permet d’utiliser le fait que \(\overline{X}_n\) suit une loi normale, et donc les résultats précédents sont applicables.
4.1.3 Intervalle de confiance pour la variance d’une loi normale
Conformément à ce qui précède, on recherche une fonction pivotale, c’est à dire une fonction des observations \(X_{1}, \ldots, X_{n}\) et de \(\sigma^{2}\), dont la loi de probabilité ne dépend ni de \(\mu\) ni de \(\sigma^{2}\). Une telle fonction est donnée par le théorème de Fisher: \(\frac{n S_{n}^{2}}{\sigma^{2}}\) est de loi \(\chi_{n-1}^{2}\).
On a donc, quels que soient les réels \(a\) et \(b\), \(0<a<b\) :
\[\begin{aligned} P\left(a \leq \frac{n S_{n}^{2}}{\sigma^{2}} \leq b\right) &=P\left(\frac{n S_{n}^{2}}{b} \leq \sigma^{2} \leq \frac{n S_{n}^{2}}{a}\right) \quad \text { d'une part } \\ &=F_{\chi_{n-1}^{2}}(b)-F_{\chi_{n-1}^{2}}(a) \quad \text { d'autre part. } \end{aligned}\]
Il y a une infinité de façons possibles de choisir \(a\) et \(b\) de sorte que cette probabilité soit égale à \(1-\alpha\). La façon la plus usuelle de procéder est d’équilibrer les risques, c’est-à-dire de prendre \(a\) et \(b\) tels que \(F_{\chi_{n-1}^{2}}(b)=1-\frac{\alpha}{2}\) et \(F_{\chi_{n-1}^{2}}(a)=\frac{\alpha}{2}\).
La table de la loi du \(\chi^{2}\) donne la valeur \(z_{n, \alpha}\) telle que, quand \(Z\) est une variable aléatoire de loi \(\chi_{n}^{2}\), alors \(P\left(Z>z_{n, \alpha}\right)=1-F_{\chi_{n}^{2}}\left(z_{n, \alpha}\right)=\alpha\).
Alors, pour \(b=z_{n-1, 1-\alpha / 2}\) et \(a=z_{n-1,\alpha / 2}\), on a bien
\[P\left(\frac{n S_{n}^{2}}{b} \leq \sigma^{2} \leq \frac{n S_{n}^{2}}{a}\right)=1-\alpha\]
D’où le résultat :
Un intervalle de confiance de seuil \(\alpha\) pour le paramètre \(\sigma^2\) de la loi \(\mathcal{N}(\mu,\sigma^2)\) est:
\[\left[\frac{n S_{n}^{2}}{z_{n-1, 1-\alpha / 2}}, \frac{n S_{n}^{2}}{z_{n-1,\alpha / 2}}\right]=\left[\frac{(n-1) S_{n}^{* 2}}{z_{n-1, 1-\alpha / 2}}, \frac{(n-1) S_{n}^{* 2}}{z_{n-1,\alpha / 2}}\right]\]
Remarque 1: \(P\left(a \leq \sigma^{2} \leq b\right)=P(\sqrt{a} \leq \sigma \leq \sqrt{b}),\) donc un intervalle de confiance de seuil \(\alpha\) pour l’écart-type \(\sigma\) est: \[ \left[\sqrt{\frac{n}{z_{n-1, 1-\alpha / 2}}} S_{n}, \sqrt{\frac{n}{z_{n-1,\alpha / 2}}} S_{n}\right] \] Remarque 2: L’intervalle de confiance est de la forme \(\left[\varepsilon_{1} S_{n}^{2}, \varepsilon_{2} S_{n}^{2}\right]\) avec \(\varepsilon_{1}<1\) et \(\varepsilon_{2}>1\) et non pas de la forme \(\left[S_{n}^{2}-\varepsilon, S_{n}^{2}+\varepsilon\right] .\) En fait, si on cherche un intervalle de confiance pour \(\sigma^{2}\) de la forme \(\left[S_{n}^{2}-\varepsilon, S_{n}^{2}+\varepsilon\right],\) la démarche ne va pas aboutir, et on ne peut pas le savoir à l’avance. C’est l’intérêt des fonctions pivotales, qui imposent d’elles-mêmes la forme de l’intervalle de confiance.
Une table de la loi de \(\chi^2\) se trouve dans l’annexe E.
4.2 Intervalle de confiance pour une proportion
Le probleme connu sous le nom d’intervalle de confiance pour une proportion est en fait le problème de la détermination d’un intervalle de confiance pour le paramètre \(p\) de la loi de Bernoulli, au vu d’un échantillon \(X_{1}, \ldots, X_{n}\) de cette loi. On a montré dans le chapitre précédent que le meilleur estimateur de \(p\) est \(\hat{P}_{n}=\overline{X}_{n}\).
Supposant que la proportion \(p\) d’individus présentant un certain caractère \(C\) (par exemple, les individus ayant voté pour un certain candidat) au sein d’une population est inconnue. Le meilleur estimateur de \(p\) est \(\hat{P}_{n}=\overline{X}_{n} = \frac{1}{n}\sum_{i=1}^n X_i\) où \(X_i\) est une v.a. de Bernoulli de paramètre \(p\), définie par:
\[X_{i}=\left\{\begin{array}{ll}{1} & {\text { si l'individu } i \text{ possède le caractère } C} \\ {0} & {\text { sinon }}\end{array}\right.\]
Comme \(X\) suit une loi de Bernoulli \(\mathcal{B}(p)\), \(n \hat{p} = \sum_{i=1}^n X_i\) suit une loi Binomiale \(\mathcal{B}(n,p)\).
Si \(n\) est faible, on utilisera les tables de la loi binomiale.
Si \(n\) est suffisamment grand5, on peut considérer (d’après le TCL6) que \(\sum_{i=1}^n X_i\) suit une loi normale \(\mathcal{N}(np, np(1-p))\), d’où \(\hat{p}_n\) suit une loi normale \(\mathcal{N}(p, \frac{p(1-p)}{n})\), et donc \(Z = \frac{\hat{p}_n - p}{\sqrt{\frac{p(1-p)}{n}}}\) suit une loi \(\mathcal{N}(0,1)\).
Le résultat précédent n’est applicable que si \(n\) est suffisamment grand.
On obtient alors, en fonction des quantiles \(P(z_{\alpha/2} \leq Z \leq - z_{\alpha/2})=1-\alpha\), l’intervalle de confiance pour \(p\):
\[IC_{1-\alpha}(p)= \Big[\hat{p}_n + z_{\alpha/2} \sqrt{\frac{p(1-p)}{n}}, \hat{p}_n - z_{\alpha/2} \sqrt{\frac{p(1-p)}{n}}\Big]\]
Cet intervalle recouvre \(p\) avec la probabilité \(1-\alpha\), mais il est toutefois inopérant puisque ses bornes dépendent de \(p\). En pratique, il existe trois façons d’obtenir l’intervalle de confiance. Nous retiendrons celle qui remplace \(p\) par son estimateur \(\hat{P}_n\). Ainsi, on obtient l’intervalle de confiance sur la proportion \(p\) en fonction de la valeur \(\hat{p}_n\) de \(\hat{P}_n\) sur notre échantillon:
\[IC_{1-\alpha}(p)= \Big[\hat{p}_n + z_{\alpha/2} \sqrt{\frac{\hat{p}_n(1-\hat{p}_n)}{n}}, \hat{p}_n - z_{\alpha/2} \sqrt{\frac{\hat{p}_n(1-\hat{p}_n)}{n}}\Big]\]
4.3 Récapitulatif pour la construction d’intervalles de confiance
Pour construire un IC, il faut d’abord déterminer le paramètre concerné par l’étude et vérifier s’il y a d’autres paramètres à estimer. Le tableau suivant résume les cas les plus communs et qui sont présentés dans ce chapitre.
| Paramètre à borner dans un IC | Symbole | Autres paramètres? | Section |
|---|---|---|---|
| Moyenne d’une loi normale | \(\mu\) | Variance \(\sigma^2\) connue | 4.1.1 |
| Moyenne d’une loi quelconque, échantillon grand | \(\mu\) | \(\sigma^2\) connue et \(n\) suffisamment grand pour appliquer TCL | 4.1.1 |
| Moyenne d’une loi normale | \(\mu\) | \(\sigma^2\) inconnue | 4.1.2 |
| Variance (ou écart-type) d’une loi normale | \(\sigma^2\) | Moyenne inconnue, mais estimée | 4.1.3 |
| Proportion | \(p\) | Rien | 4.2 |