D Table de la loi de Student

Attention pour la description de cette table. Ici on donne directement le quantile \(t_{n,1-\frac{\alpha}{2}}\).

\(X\) étant une variable aléatoire de loi de Student à \(n\) degrés de liberté \(St(n)\) et \(\alpha\) un réel de \([0,1]\), la table donne la valeur de \(t_{n,1-\frac{\alpha}{2}} = F^{-1}(1-\frac{\alpha}{2})\) telle que \(P(|X| > t_{n,1-\frac{\alpha}{2}})=\alpha\). En , la commande correspondante est qt(1-alpha/2, n).

#ans> Error in loadNamespace(x): there is no package called 'shape'
#ans> Error in loadNamespace(x): there is no package called 'shape'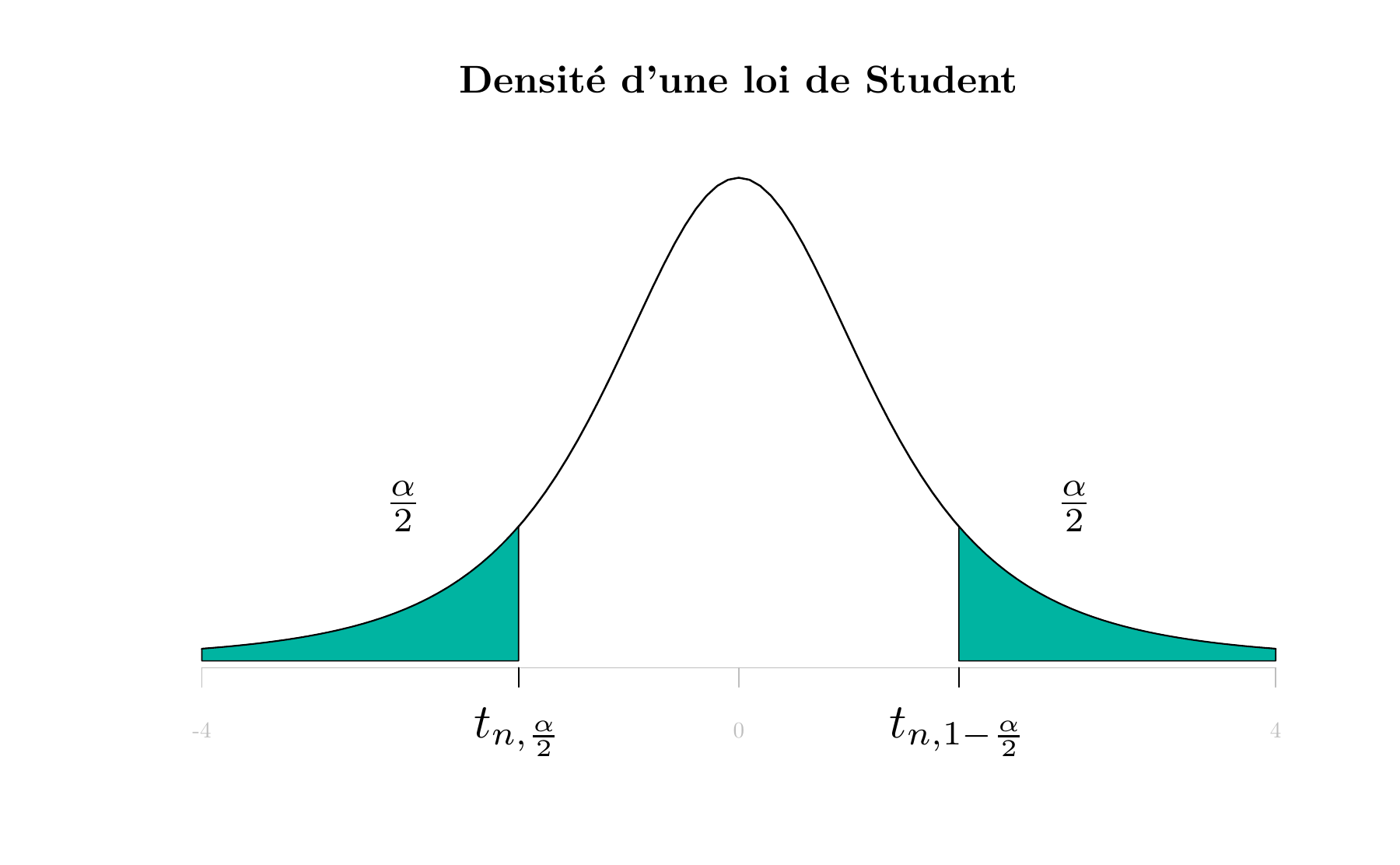

\(n \backslash \alpha\)	0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.2	0.1	0.05	0.02	0.01	0.001
1	0.158	0.325	0.510	0.727	1.000	1.376	1.96	3.08	6.31	12.71	31.82	63.66	636.62
2	0.142	0.289	0.445	0.617	0.816	1.061	1.39	1.89	2.92	4.30	6.96	9.93	31.60
3	0.137	0.277	0.424	0.584	0.765	0.978	1.25	1.64	2.35	3.18	4.54	5.84	12.92
4	0.134	0.271	0.414	0.569	0.741	0.941	1.19	1.53	2.13	2.78	3.75	4.60	8.61
5	0.132	0.267	0.408	0.559	0.727	0.920	1.16	1.48	2.02	2.57	3.37	4.03	6.87
6	0.131	0.265	0.404	0.553	0.718	0.906	1.13	1.44	1.94	2.45	3.14	3.71	5.96
7	0.130	0.263	0.402	0.549	0.711	0.896	1.12	1.42	1.90	2.37	3.00	3.50	5.41
8	0.130	0.262	0.399	0.546	0.706	0.889	1.11	1.40	1.86	2.31	2.90	3.35	5.04
9	0.129	0.261	0.398	0.543	0.703	0.883	1.10	1.38	1.83	2.26	2.82	3.25	4.78
10	0.129	0.260	0.397	0.542	0.700	0.879	1.09	1.37	1.81	2.23	2.76	3.17	4.59
11	0.129	0.260	0.396	0.540	0.697	0.876	1.09	1.36	1.80	2.20	2.72	3.11	4.44
12	0.128	0.259	0.395	0.539	0.695	0.873	1.08	1.36	1.78	2.18	2.68	3.06	4.32
13	0.128	0.259	0.394	0.538	0.694	0.870	1.08	1.35	1.77	2.16	2.65	3.01	4.22
14	0.128	0.258	0.393	0.537	0.692	0.868	1.08	1.34	1.76	2.14	2.62	2.98	4.14
15	0.128	0.258	0.393	0.536	0.691	0.866	1.07	1.34	1.75	2.13	2.60	2.95	4.07
16	0.128	0.258	0.392	0.535	0.690	0.865	1.07	1.34	1.75	2.12	2.58	2.92	4.01
17	0.128	0.257	0.392	0.534	0.689	0.863	1.07	1.33	1.74	2.11	2.57	2.90	3.96
18	0.127	0.257	0.392	0.534	0.688	0.862	1.07	1.33	1.73	2.10	2.55	2.88	3.92
19	0.127	0.257	0.391	0.533	0.688	0.861	1.07	1.33	1.73	2.09	2.54	2.86	3.88
20	0.127	0.257	0.391	0.533	0.687	0.860	1.06	1.32	1.73	2.09	2.53	2.85	3.85
21	0.127	0.257	0.391	0.532	0.686	0.859	1.06	1.32	1.72	2.08	2.52	2.83	3.82
22	0.127	0.256	0.390	0.532	0.686	0.858	1.06	1.32	1.72	2.07	2.51	2.82	3.79
23	0.127	0.256	0.390	0.532	0.685	0.858	1.06	1.32	1.71	2.07	2.50	2.81	3.77
24	0.127	0.256	0.390	0.531	0.685	0.857	1.06	1.32	1.71	2.06	2.49	2.80	3.75
25	0.127	0.256	0.390	0.531	0.684	0.856	1.06	1.32	1.71	2.06	2.48	2.79	3.73
26	0.127	0.256	0.390	0.531	0.684	0.856	1.06	1.31	1.71	2.06	2.48	2.78	3.71
27	0.127	0.256	0.389	0.531	0.684	0.855	1.06	1.31	1.70	2.05	2.47	2.77	3.69
28	0.127	0.256	0.389	0.530	0.683	0.855	1.06	1.31	1.70	2.05	2.47	2.76	3.67
29	0.127	0.256	0.389	0.530	0.683	0.854	1.05	1.31	1.70	2.04	2.46	2.76	3.66
30	0.127	0.256	0.389	0.530	0.683	0.854	1.05	1.31	1.70	2.04	2.46	2.75	3.65
40	0.126	0.255	0.388	0.529	0.681	0.851	1.05	1.30	1.68	2.02	2.42	2.70	3.55
80	0.126	0.254	0.387	0.526	0.678	0.846	1.04	1.29	1.66	1.99	2.37	2.64	3.42
120	0.126	0.254	0.386	0.526	0.677	0.845	1.04	1.29	1.66	1.98	2.36	2.62	3.37
\(+\infty\)	0.126	0.253	0.385	0.524	0.674	0.842	1.04	1.28	1.64	1.96	2.33	2.58	3.29